Уравнение Шредингера

Важнейшим является спектр собственных значений оператора полной энергии 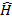. Для одной частицы в заданном внешнем по­тенциальном поле оператор полной энергии (называемый опера­тором Гамильтона, или гамильтонианом)

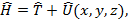(1,8)

где - оператор кинетической энергии; - оператор потенциальной энергии частицы.

Уравнение для его собственных функций Ψ и собственных зна­чений ε имеет вид

или (1.9)

Это одно из основных уравнений квантовой механики, назы­ваемое уравнением Шредингера для стационарных состояний.

Конкретизируя в каждой из рассматриваемых задач физиче­скую природу и особенности взаимодействия, можно установить зависимость потенциальной энергии U от координат. Решение урав­нения (1.9) при учете граничных условий дает весь набор соб­ственных значений и собственных функций оператора 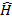, т. е. все возможные значения энергии физической системы. При этом для состояний, которые отвечают так называемому финитному дви­жению, т. е. движению частиц в ограниченной области простран­ства, спектр значений энергии получается дискретным. Если об­ласть, в которой могут быть обнаружены частицы, неограничен­но велика, то энергия может меняться непрерывно.

Переход к анализу состояний позволяет не анализировать при­чины, происходящие в каждом конкретном акте взаимодействия, а перейти к усреднению соответствующих величин по времени и пространству. Предполагается, что именно эти усредненные зна­чения параметров состояния и фиксируются в эксперименталь­ных исследованиях, поэтому их использование в уравнениях по­зволяет описывать реальные явления.

При одной и той же форме оператора потенциальной энергии спектры могут быть как дискретными, так и сплошны­ми (непрерывными). Так, электронные состояния в кулоновском поле атомного ядра могут иметь как дискретный, так и непрерыв­ный энергетические спектры. Первый соответствует классическо­му движению по эллиптическим орбитам, а второй - движению по незамкнутым параболическим или гиперболическим орбитам. Какой из этих вариантов реализуется, определяется значением энергии.

Обычно функция Ψ(x,t)определяется из выражения для плот­ности вероятности нахождения частицы в точке х в момент времени t:

Плотность вероятности = (1.10)

В общем случае Ψ - величина комплексная. Так как вероятность должна быть величиной действительной, для нахождения плотнос­ти вероятности необходимо умножить Ψ на комплексно сопряжен­ную с ней функцию Ψ *(x,t). Поскольку Ψ *(х, t)Ψ(х, t)dx есть вероят­ность того, что частица находится в интервале от х до (х + dx) в момент времени t и поскольку вероятность нахождения частицы в какой-либо точке пространства в некоторый момент времени tравна единице, то

. (1.11)

Отказавшись от описания движения частицы с помощью тра­екторий, получаемых из законов Ньютона, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение урав­нение, эквивалентное законам Ньютона и дающее рецепт для нахождения Ч' в частных физических задачах. Как было сказано ранее, таким уравнением является уравнение Шредингера. В од­номерном случае оно имеет вид

+U(x)Ψ(x,t)=- 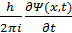, (1.12)

где h - постоянная Планка; т - масса частицы; U(x)- потенци­альная энергия частицы в точке х.

Уравнение (1.12) записано в одномерном представлении для упрощения.

Уравнение Шредингера вводится без какого-либо вывода и вообще не может быть выведено из более простых представле­ний точно так же, как не могут быть выведены из каких-либо простых законов законы Ньютона. Уравнение Шредингера явля­ется просто законом физики и если оно имеет смысл, то должно приводить к правильному предсказанию экспериментальных дан­ных. Квантовая теория не требует полного отказа от законов Ньютона, а лишь настаивает на отказе от абсолютной опреде­ленности в задании начальных условий. Если размер и масса ча­стицы становятся макроскопическими, то предсказания кванто­вой и классической теории совпадают друг с другом, потому что неопределенный путь частицы становиться близким к однознач­ной траектории.

Форма уравнения Шредингера показывает, что относительно времени его решение должно быть простым, поскольку время вхо­дит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда Uне является функцией времени, можно записать в виде

Ψ(x,t)=Ψ(x)·exp (1.13)

где функция Ψ(x)должна удовлетворять (в одномерном случае) уравнению

+U(x)Ψ(x,t)=EΨ(x),

которое получается из уравнения (1.12) при подстановке в него уравнения (1.13).

Уравнение (1.14) вообще не содержит времени; в связи с этим оно называется уравнением Шредингера, не содержащим време­ни. Выражение (1.13) является лишь частным решением зависящего от времени уравнения Шредингера (l.11). Зависимость функции Ψ (х, t) от времени проста, но зависимость ее от координаты не всегда имеет элементарный вид, так как уравнение (1.14) при од­ном выборе вида потенциальной функции U (х, t) совершенно от­личается от того же уравнения при другом выборе этой функции. В действительности уравнение (1.14) может быть решено аналити­чески лишь для небольшоro числа частных типов функции U (х).

Важное значение имеет интерпретация величины Е в уравне­нии (1.13). Она производится следующим путем: временная зави­симость функции Ψ (х,t) в уравнении (1.13) имеет экспоненци­альный характер, причем коэффициент при t в показателе экспо­ненты выбран так, что правая часть уравнения (1.14) содержит просто постоянный множитель Е. В левой части уравнения (1.14) функция Ψ умножается на потенциальную энергию U (х). Следова­тельно, из соображений размерности следует, что величина Е должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы. Таким образом, мож­но предполагать, что величина Е представляет собой полную энер­гию. Согласно физической интерпретации уравнения Шредингера Е действительно является полной энергией частицы при движе­нии, описываемом функцией Ψ (х, t).

Поиск по сайту: