 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Расчет энергии связи двух атомов
После того, как мы с известной долей вероятности выяснили, как устроено твердое тело (кристаллическое или аморфное), нужно понять, почемуоно так устроено, какие силы объединяют атомы в структуру твердого тела. Проблема связи атомов в телах вследствие одинаковой природы сил взаимодействия между атомами аналогична проблеме связи атомов в молекуле. Рассмотрим два атома: А и В.При достаточно большом расстоянии между ними они ведут себя, естественно, как свободные. Энергия такой системы, состоящей из двух изолированных атомов, равна сумме энергий этих атомов, которую можно произвольно принять за нуль. Атомы не взаимодействуют друг с другом до тех пор, пока расстояние rмежду ними велико по сравнению с величиной (ra+rb), где ra и rb - радиусы атомов А и В. Если при уменьшении расстояния между атомами энергия системы понижается по сравнению с суммарной энергией изолированных атомов, то между атомами возникает сила притяжения. Это соответствует уменьшению потенциaльнoй энергии системы U(r). При некотором расстоянии r=r0 энергия U(r)достигает минимального значения, которое соответствует силе F:
 . (1.43)
. (1.43)
Этот минимум обязательно существует; в противном случае вообще не могла бы образоваться молекула с конечным расстоянием между ядрами.
При дальнейшем сближении атомов между ними начинают действовать силы отталкивания, которые быстро возрастают с уменьшением r, что сопровождается возрастанием потенциальной энергии U(r). Смена притяжения отталкиванием может быть приближенно описана путем представления полной потенциальной энергии взаимодействия в виде суммы двух членов, из которых один член (отрицательный) соответствует энергии сил притяжения, а другой (положительный) - энергии сил отталкивания:
 (1.44)
(1.44)
На рис. 1.10 изображены кривые этих потенциалов и суммарная кривая, соответствующая полной потенциальной энергии взаимодействия. При расстоянии  , соответствующем минимуму энергии системы, силы притяжения уравновешиваются силами отталкивания; при этом образуется молекула АВс наиболее стабильной конфигурацией, в которой ядра атомов совершают колебания с собственной частотой ω0. Вблизи положения равновесия форма кривой U=U(r)близка к параболе, как это видно из разложения U(r)в ряд Тейлора в окрестности
, соответствующем минимуму энергии системы, силы притяжения уравновешиваются силами отталкивания; при этом образуется молекула АВс наиболее стабильной конфигурацией, в которой ядра атомов совершают колебания с собственной частотой ω0. Вблизи положения равновесия форма кривой U=U(r)близка к параболе, как это видно из разложения U(r)в ряд Тейлора в окрестности  :
:
 (1.45)
(1.45)
| Uотт |
| r0 |
| r |
| U |
| Uпр |
| Рисунок 1.10. Зависимость полной потенциальной энергии взаимодействия двух атомов (сплошная кривая) от расстояния между ними |
Из выражения (1.45) следует, что при не очень больших отклонениях атома от положения равновесия (когда третьим членом можно пренебречь) возвращающая сила пропорциональна расстоянию и атомы колеблются как гармонические осцилляторы. Энергетические уровни такого осциллятора, как это следует из квантовой механики, могут быть получены из следующего выражения:
 (1.46)
(1.46)
Глубина минимума U0равна энергии связи атомов в молекуле. Энергия связи, или энергия сцепления, равна разности потенциальной энергии системы в начальном (1) и конечном (2) состояниях:
U=U1-U2. (1.47)
За начальное состояние системы обычно принимают такое состояние, когда частицы (атомы, молекулы, ионы) находятся друг от друга на достаточно больших расстояниях и не взаимодействуют между собой, так что можно принять U1=0.
Конечное состояние отвечает равновесному расположению частиц системы при Т=0К. Следовательно, энергию связи можно представить в виде U=-U2.С учетом нулевых колебаний с частотой ω0 определится энергия связи для молекулы U0-  /2=U0-E0, как показано на рис. 1.10.
/2=U0-E0, как показано на рис. 1.10.
Для оценки энергии связи необходимо знать хотя бы в общем виде зависимости потенциалов притяжения и отталкивания от расстояния между взаимодействующими атомами. Конкретный вид этих зависимостей определяется природой взаимодействующих атомов. Исходя из электростатического характера сил притяжения их потенциал можно представить в виде степенной функции:
 (1.48)
(1.48)
где а - положительная константа; т - показатель степени r, имеющий также положительное значение.
При m= 1 потенциал сил притяжения соответствует обычному кулоновскому взаимодействию между противоположно заряженными ионами, а при m=6 - потенциалу притяжения между атомами инертных газов.
Для потенциала сил отталкивания, который обусловлен прежде всего отталкиванием ядер взаимодействующих атомов и зависит от экранировки ядер окружающими их электронами, М. Борн и А. Ланде исходя из классических представлений вывели выражение
 (1.49)
(1.49)
где b, п > 0 - постоянные; r - расстояние между центрами взаимодействующих атомов.
При выводе формулы для потенциала сил отталкивания М. Борном и А. Ланде была выбрана статическая модель атома, в которой электроны в 8-электронной оболочке размещены по вершинам куба. Совершенно очевидно, что при взаимодействии таких атомов потенциал сил отталкивания должен зависеть от их взаимной ориентации, но это никогда не подтверждается экспериментально. Трудно представить себе атом, имеющий форму кубика, особенно в свете планетарной модели Бора или модели электронных оболочек.
Квантово- механический расчет, в котором точечное распределение электронов заменено распределением, описываемым квадратом модуля волновой функции 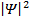 , выполненный М. Борном и М. Г. Майером, привел для потенциала сил отталкивания к полуэмпирическому выражению, которое лучше согласуется с экспериментом:
, выполненный М. Борном и М. Г. Майером, привел для потенциала сил отталкивания к полуэмпирическому выражению, которое лучше согласуется с экспериментом:
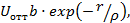 (1.50)
(1.50)
где b, ρ - постоянные.
Хотя формула Борна - Майера лучше описывает реальность, предпочитают пользоваться формулой Борна - Ланде, поскольку это значительно упрощает расчеты, т. е. «ищут не там где потеряли, а там, где светлее и удобнее, - под фонарем».
Выражение для полной потенциальной энергии взаимодействия двух атомов запишем в виде:
 (1.51)
(1.51)
Для того чтобы Функция ив этом выражении имела минимум, необходимо, чтобы показатель степени потенциала отталкивания был больше показателя степени потенциала притяжения, т. е. чтобы выполнялось условие п > т. Попытаемся найти равновесное расстояние r0 из условия минимума энергии 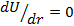 :
:
 (1.52)
(1.52)
Подставив  в формулу (1.51), найдем выражение для энергии сцепления двухатомной молекулы:
в формулу (1.51), найдем выражение для энергии сцепления двухатомной молекулы:
 (1.53)
(1.53)
Так как n > m, то из выражения (1.53) следует, что энергия сцепления в основном определяется потенциалом сил притяжения, а потенциал сил отталкивания является лишь небольшой добавкой к нему. Это связано с тем, что потенциал сил отталкивания возрастает настолько круто при уменьшении r, что его вклад в полную энергию в минимуме функции U(r)становится относительно малым.
Зависимость энергии связи в кристаллах от межатомного расстояния r, так же как и в молекулах, определяется двумя главными членами: 1) притяжением атомов, обусловленным взаимодействием валентных электронов; 2) кулоновским отталкиванием внутренних оболочек атомных остовов и отталкиванием ядер. Для устойчивого равновесного состояния  обязательно наличие минимума энергии на суммарной кривой энергий притяжения и отталкивания, который соответствует определенной стабильной конфигурации в расположении атомов кристаллической решетки.
обязательно наличие минимума энергии на суммарной кривой энергий притяжения и отталкивания, который соответствует определенной стабильной конфигурации в расположении атомов кристаллической решетки.
Энергия связи (или энергия сцепления)кристалла представляет собой энергию, которая необходима для разделения тела на составные части. В зависимости от типа твердого тела составными частями могут быть молекулы и атомы в молекулярных кристаллах, атомы в ковалентных и металлических кристаллах, положительно и отрицательно заряженные ионы в ионных кристаллах.
При расчете энергии сцепления молекулярных и ионных кристаллов в силу того, что конфигурация электронов в этих кристаллах не очень сильно отличается от их конфигурации в изолированных атомах или ионах, обычно ограничиваются вычислением классической потенциальной энергии системы сферически симметричных частиц, образующих определенную кристаллическую структуру. Считается, что силы, действующие между атомами или ионами, являются центральными, т. е. полная потенциальная энергия системы зависит только от расстояния между взаимодействующими частицами, которые локализованы в узлах решетки и кинетическая энергия которых пренебрежимо мала. Даже при таких грубых приближениях теоретические оценки энергии связи приводят к удовлетворительному соответствию с экспериментом.
Если предположить, что энергия взаимодействия двух частиц (атомов или ионов) системы не зависит от присутствия других частиц, то для кристалла, в котором конфигурации и энергетические состояния эквивалентных частиц одинаковы (за исключением частиц, лежащих в поверхностном слое), можно найти энергию взаимодействия любого атома со всеми остальными атомами, а затем и полную потенциальную энергию кристалла. Пусть 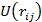 - потенциальная энергия взаимодействия между двумя частицами (i и j) в кристалле, расстояние между которыми равно
- потенциальная энергия взаимодействия между двумя частицами (i и j) в кристалле, расстояние между которыми равно  Выбрав в объеме кристалла цeнтp i-й частицы за начало отсчета и просуммировав по всем остальным частицам при
Выбрав в объеме кристалла цeнтp i-й частицы за начало отсчета и просуммировав по всем остальным частицам при  , найдем энергиювзаимодействия i-йчастицы со всеми другими частицами решетки:
, найдем энергиювзаимодействия i-йчастицы со всеми другими частицами решетки:
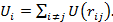 (1.54)
(1.54)
Аналогичную процедуру проделываем для всех оставшихся (N-1) частиц. Тогда полная потенциальная энергия решетки кристалла, содержащего N частиц, определится по формуле
 . (1.55)
. (1.55)
Предполагается, что N достаточно велико, чтобы можно было пренебречь поверхностными эффектами. В формуле (1.55) множитель 1/2 появляется потому, что при суммировании производится учет энергии взаимодействия каждой пары частиц дважды. Выражение (1.55) для потенциальной энергии справедливо как для однородных, так и для неоднородных систем.
Все приведенные ранее рассуждения и результаты справедливы лишь для расчета энергии сцепления молекулярных и ионных кристаллов. Для ковалентных кристаллов и металлов, в которых конфигурации валентных электронов значительно отличаются от их конфигурации в изолированных атомах, уже недостаточно классических представлений и необходимо привлечение квантово-механических представлений.
Поиск по сайту: