 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Квантование энергии. Частица в потенциальном ящике
Из уравнения Шредингера можно вывести одно из фундаментальных положений квантовой механики - положение о квантовании энергии. Рассмотрим одномерное движение частицы; ограничим это движение пределами ящика: 0  . Пусть потенциальная энергия бесконечна при х < 0 и х> L и равна нулю при 0
. Пусть потенциальная энергия бесконечна при х < 0 и х> L и равна нулю при 0  (рис. 1.1). Уравнением Шредингера для области 0
(рис. 1.1). Уравнением Шредингера для области 0  является по-прежнему уравнение (1.17), а решением его - полученная ранее экспоненциальная функция. Однако теперь Ψ-функция должна быть равна нулю при х = 0 и при всех отрицательных значениях х, поскольку частица не может перескочить через стенки ящика.
является по-прежнему уравнение (1.17), а решением его - полученная ранее экспоненциальная функция. Однако теперь Ψ-функция должна быть равна нулю при х = 0 и при всех отрицательных значениях х, поскольку частица не может перескочить через стенки ящика.
Указанная функция должна также равняться нулю и при всех значениях х, превышающих х = L. Искомая функция представляет собой некоторую комбинацию синусов и косинусов:
| L |
| x |
U= 
|
U= 
|
| U=0 |
| Рис. 1.1. Потенциальная энергия частицы в одномерном потенциальном ящике |
 (1.22)
(1.22)
Поскольку в точке х = О косинус не равен нулю, тогда как синус обращается в нуль, Ψ-функция должна быть синусоидальной функцией. Решение необходимо ограничить также рассмотрением лишь таких синусоидальных функций, которые обращаются в нуль при х> L.
Аналитически требование, налагаемое на функцию в точке х = L, выражается следующим образом:
 (1.23)
(1.23)
Согласно уравнению (1.23) k может принимать не все значения; разрешенными значениями являются лишь те, для которых выполняется условие
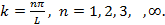 (1.24)
(1.24)
Если волновой вектор k может пробегать лишь последовательность дискретных значений, то энергия частицы также дискретна, т. е. она квантуется:
| E1 |
| n=1 |
| E |
| n=2 |
| n=3 |
| 4E1 |
| 9E1 |
| Рис. 1.2. Энергетический спектр частицы |
 (1.25)
(1.25)
Смысл выражения (1.25) заключается в том, что частица, движущаяся в потенциальном ящике, может обладать не произвольным значением энергии, а лишь одним значением из набора дискретных значений. Энергия, таким образом, обладает дискретным спектром, который показан на рис. 1.3. Причину того, что энергия совершенно свободной частицы не квантована, можно легко понять, проанализировав выражение (1.25). Если длина потенциального ящика бесконечно увеличивается, то расстояние между энергетическими уровнями становится бесконечно малым. В общем случае, согласно квантовой механике, несвязанные частицы, которые можно считать практически свободными, имеют непрерывный энергетический спектр, тогда как частицы, которые удерживаются какими-либо силами в конечной области пространства, обладают дискретным энергетическим спектром.
Один из аспектов проведенного обсуждения дозволенных решений может вызвать сомнения. Предполагается, что волновая функция обращается в нуль при х = О и х = L, так как вне этих пределов она должна равняться нулю. Волновые функции, следовательно, непрерывны на стенках ящика, но их первые производные терпят разрыв. Тогда возникает вопрос: почему функция не может сама быть разрывной на стенках ящика? Причина, по которой функции такого вида не могут быть выбраны, не очевидна, пока не проделаны дальнейшие расчеты последствий такого выбора. Такие вычисления показывают, что если Ψ-функция терпит в некоторой точке разрыв, то скорость частицы в этой точке оказывается бесконечно большой, а следовательно, бесконечна и кинетическая энергия. Поскольку предполагается, что полная энергия частицы не может быть бесконечно большой, такое решение физически неприемлемо. Таким образом, энергия квантуется по той причине, что только определенные Ψ-функции имеют физический смысл, т. е. энергия не могла бы сохраняться во время движения в потенциальном ящике частицы с некорректно заданной энергией.
Нарушение непрерывности производной от волновой функции на границах потенциального ящика возможно потому, что такое поведение Ψ-функции соответствует действию на частицу бесконечно большой силы. Поскольку стенка потенциального ящика непроницаема для частиц, мгновенная сила, действующая со стороны ящика на частицу в момент ее удара о стенку, является бесконечно большой, но в то же время чрезвычайно кратковременной.
Квантование энергии является следствием необходимости физически оправданного выбора решений уравнения Шредингера. Поскольку уравнение Шредингера обусловлено принципом неопределенности, покажем, что минимум энергии спектра (см. рис. 1.2) действительно предсказывается принципом неопределенности. Если частица заключена в потенциальный ящик, наибольшее возможное значение неопределенности в изменении положения частицы равно ширине этого ящика. Следовательно, ∆x = L. Пусть частица обладает импульсом р. Поскольку частица должна отскакивать после соударения от стенки к стенке, неопределенность в определении величины импульса частицы, заключенной в ящике, должна равняться 2р, так как при ударах о стенки импульс меняется от значения +р до значения -р и обратно. Следовательно, соотношение неопределенностей для максимально нелокализованной частицы (обладающей минимальной энергией) имеет вид
(∆x)(∆p)=(L)(2p)=h. (1.26)
С учетом соотношения  для энергии получаем выражение
для энергии получаем выражение
 , (1.27)
, (1.27)
которое совпадает с формулой (1.25) при п = 1.
Поиск по сайту: