МЕТОДИЧНІ ПОРАДИ

3.4.5 Практикум 4 Коефіцієнт кореляції рангів

Коефіцієнт кореляції являє собою показник, за допомогою якого вимірюється тіснота зв’язку (Загальна ідея кореляції була значною мірою обгрунтована вченим-біологом Френсісом Гальтоном у 80-х роках ХІХ ст. Однак той показник кореляції, що використовується в даний час, а саме коефіцієнт кореляції “добуток моментів”, був введений Карлом Пірсоном в 1898 р.).

Припустимо, що ви тільки що одружились, і перед вашою молодою сім’єю виникла така проблема: вам дуже хочеться мати дитину, однак в той же час ви стурбовані проблемами демографічного вибуху, зростанням безробіття, відсутністю житла. Як ви вчините у цьому випадку: постараєтесь задовольнити власне бажання чи відмовитесь від своїх намірів. Якщо є впевненість, що в майбутньому, після закінчення деякого більш чи менш тривалого періоду часу, наш світ стане кращим завдяки самовідданим зусиллям вашого, який знаходиться поки ще в проекті, нащадка, то у вас будуть всі підстави для того, щоб подарувати йому життя; в противному разі краще залишитися бездітним. Якими ж якостями повинна володіти людина, яка зможе якимсь чином покращити наш світ? Майже кожен в стані дати відповідь на це запитання: така людина повинна бути чесною, доброю, дружелюбною, ввічливою, дисциплінованою, енергійною, сміливою, розумною тощо.

Але чи можливо завбачити, що всіма цими якостями буде володіти ще ненароджена дитина? Якщо ваш коефіцієнт розумового розвитку IQ рівний 125, а вашої дружини 135, то чи означає це, що ваша майбутня дитина виросте кмітливою і її коефіцієнт IQ складе 130 (середнє з двох коефіцієнтів)?

Якщо ви проконсультуєтесь у соціолога, то він вам пояснить що ситуація в дійсності дещо складніша, ніж вам здається. Так, є позитивна кореляція (її значення рівне приблизно +0,60) між середньою величиною показника IQ батьків і значенням цього ж показника їх дитини, звідки виходить, що ваша дитина, можливо, буде володіти інтелектуальними здібностями, вищими за середній рівень. Однак необхідно розглянути ще цілий ряд моментів: регресію до середньої, вибірковий розподіл прогнозуючих значень IQ і стандартну помилку будь-якого прогнозу. Підбадьорені і в той же час дещо збентежені такою відповіддю, ви наважуєтесь зробити таке: по-перше, прикласти всі необхідні зусилля, щоб все-таки мати дитину, і, по-друге, прочитати решту порад, щоб зняти смагу таємничості з термінології, якою користується соціолог.

Якщо дві будь-які характеристики, одержані для одного і того ж “об’єкта”, мають тенденцію змінюватись разом, так що створюється можливість передбачати величину для однієї з них за значенням іншої, то кажуть, що ці характеристики корелюють одна з одною. Подібний приклад ми вже розглянули – кореляція між середнім показником IQ батьків і середньою величиною цього ж показника у їх дітей. “Об’єкт” у даному випадку являє собою якусь одиницю, яку утворюють батьки і їх діти. Це означає, що існує можливість передбачати величину коефіцієнта IQ дітей за значенням цього показника у їх батьків.

Таким чином, спостерігається тенденція, у відповідності з якою у батьків, які мають високий показник IQ, будуть народжуватись діти також з високим рівнем цього показника, і, навпаки, батьки з низьким IQ будуть мати дітей з рівнем інтелекту нижче середнього. Загалом величина дитячих показників IQ має тенденцію відповідати значенням коефіцієнтів розумового розвитку їх батьків. Якою відповідати – це залежить від величини коефіцієнта кореляції даного взаємозв’язку.

Коефіцієнт кореляції являє собою число, знак і величину якого характеризує напрямок і силу подібного взаємозв’язку. Є дуже багато різних типів коефіцієнтів кореляції, однак у даний час на практиці найчастіше використовується коефіцієнт кореляції добутку моментів Пірсона, який позначається літерою r.

Значення коефіцієнта кореляції можуть змінюватись від –1,0 до +1,0 (включаючи значення 0,0).Знак коефіцієнта вказує на напрямок – прямий або обернений – взаємозв’язку між двома змінними. Абсолютне значення коефіцієнта (без врахування знака) характеризує силу, або тісноту досліджуваного взаємозв’язку. Коефіцієнт кореляції, рівний плюс або мінус 1,0, вказує на наявність строгого функціонального взаємо-зв’язку. Значення коефіцієнта 0,0 свідчить про відсутність будь-якого взаємозв’язку між досліджуваними змінними.

У випадку, коли високим значенням однієї змінної відповідають високі значення іншої змінної, а низьким значенням низькі, кореляція між цими змінними позитивна. Розглянемо декілька прикладів.

1. Як відомо, існує позитивна кореляція між коефіцієнтами IQ батьків і їх дітей.

2. Ще сильніший позитивний кореляційний взаємозв’я-зок проявляється між коефіцієнтами IQ близнюків; іншими словами, значення коефіцієнтів IQ близнюків звично виявляються майже рівними.

3. Дані в різних регіонах свідчать про існування позитивної кореляції між середньою величиною доходу і числом злочинів проти власності і майна громадян та організацій. Цей факт суперечить теоретичним уявленням деяких соціологів, які стверджують, що рівень бідності і рівень злочинності змінюються в одному і тому ж напрямку.

4. Проявляється сильна позитивна кореляція між смаковими якостями витриманих вин і їх ціною. Загалом чим вище оцінюється якість вина дегустатором, тим вища ціна.

Негативна кореляція має місце там, де високим значенням однієї змінної відповідають низькі значення іншої змінної. І знову розглянемо декілька прикладів.

1. Для початку пошлемось на найпоширеніше висловлювання наших мам, яке вони вживають, коли говорять про наші вчинки або наміри, які їм не дуже до вподоби: “Чим більше я про це думаю, тим менше тебе розумію”.

2. Як більш формальний приклад відзначимо негативний зв’язок між швидкістю і точністю виконання завдання. Чим швидше людина виконує завдання, тим нижча точність її дій, і навпаки, чим менша швидкість, тим вища точність виконання завдання.

3. Проявляється негативна кореляція між кількістю домовласників і кількістю багатодітних сімей, що проживають в одному і тому ж районі. Багатодітні сім’ї мають низький рівень доходу і, отже, не володіють засобами, достатніми для придбання власного будинку.

4. Приклад, стосовно географії. Дані про адміністративний поділ Великобританії свідчить про існування негативного кореляційного зв’язку між площею садово-паркової зони і числом нещасних випадків, чим більша садово-паркова зона, тим менша кількість нещасних випадків серед дітей у цьому районі.

Абсолютне значення коефіцієнта кореляції характеризує тісноту взаємозв’язку. Коефіцієнти кореляції у деяких наведених прикладах відповідно рівні: між рівнем доходу і рівнем злочинності +0,50; між якістю вина і його ціною +0,85; між числом великих сімей і числом власників – 0,65; між площею садово-паркової зони і кількістю нещасних випадків – 0,86.З наведених коефіцієнтів найбільшим є останній. Таким чином, тіснота взаємозв’язку визначається абсолютною величиною коефіцієнта кореляції.

При вивченні ознак соціологу інколи буває важко виразити їх одиницями будь-якої розмірності для кількісного вимірювання. Однак він може відзначити наявність більшої чи меншої кількості будь-якої властивості в явищі, правда, не з такою точністю, як встановити вік або відсоток виконання норм виробітку чи бюджет вільного часу, а всього лише наближено з певною допустимою точністю. Наприклад, культурний рівень кожного з групи осіб можна виразити за допомогою балів, але ця оцінка буде досить наближеною.

Індивідів з присвоєною їм кількістю балів можна розмістити в порядку зменшення або зростання балів чи номерів, тобто ранжувати, тоді номер кожного індивіда буде його рангом.

У своїх дослідженнях ми зробили спробу проранжувати числа, що виражають наявність ознаки в кожних 100 респондентів в різних типологічних групах.

Наприклад, ми взяли приблизно рівні групи робітників за професіями і встановили кількість осіб (на 100 чоловік), які відповіли, що вони вважають свою роботу цікавою. Відтак у цих групах визначили кількість осіб (на 100 чоловік), які назвали мотивом свого вибору цікавість для спеціальності. Якщо приймемо гіпотезу, що між вибором спеціальності в силу інтересу до неї і інтересом до виконуваної роботи є причинно-наслідковий зв’язок, то, мабуть, при зростанні частот у відповідях “спеціальність цікавить” повинні зростати частоти і у відповідях “цікава робота” і навпаки. Не дивля-чись на деякі коливання, загалом проявляється певна тенденція, а саме зі зростанням частот у другій колонці зростають частоти в третій колонці.

Таким чином, якщо є ряд індивідів чи різних груп осіб, проранжованих за двома різними ознаками, то ранги можуть дати деяку міру тісноти зв’язку між цими двома ознаками, факторами, властивостями. Якби колонки збігались повністю, тобто, якби колонки в третій колонці були розміщені в такій же строгій послідовності, як і в другій, то зв’язок між цими ознаками був би, мабуть, дуже тісним і навпаки.

Інтерпретація коефіцієнта кореляції. Щоб зрозуміти, яким чином коефіцієнт кореляції відображає тісноту зв’язку x і y, припустимо, що лінійне рівняння y=3x+10 обране як моделі для описання даних табл. 3.13. За допомогою цього рівняння будь-якому частковому значенню x, скажімо, х’ можемо поставити у відповідність розрахункове значення y’, а саме: y’=3x’+10. Наприклад, коли х’=1, y’=13. В цьому випадку розходження між фактичним і розрахунковим значеннями y буде дорівнювати (y-3х’-10). Це відхилення розрахункового значення від фактичного зветься “залишком”, а дисперсія подібних відхилень називається “дисперсією залишків”. Відхилення п’яти пар спостережень від рівняння y=3x+10 дорівнюють 4, -5, 7, -3, 2, а дисперсія залишків складає 27,75 (відповідно стандартне відхилення залишків дорівнює 5,1).

Таблиця 3.13 — П’ять пар спостережень x і y

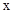
Якщо зв’язок між x і y буде сильним, то дисперсія залишків буде мати відносно невелике значення порівняно з дисперсією y (тобто середнім квадратом відхилень факторних значень y від їх загальної середньої 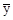). І це знайде своє відображення у високому значенні коефіцієнта кореляції. Зв’язок між цими показниками виглядає так: квадрат коефіцієнта кореляції дорівнює 1 мінус відхилення дисперсії залишків до дисперсії y, тобто:

r² = .

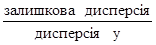Дане співвідношення може бути переписане по-іншому: дисперсія залишків =(1-r²) дисперсія y.

Отже, коефіцієнт (1-r²) характеризує собою ступінь відхилення фактичних значень у від теоретичних. Те ж саме можна виразити інакше, якщо сказати, що х “пояснює” рівну r² частку дисперсії у, а залишкова частка (1-r²) дисперсії зумовлена впливом “неврахованих факторів”.

Для того, щоб використати не стільки абстрактні міри розсіву, як дисперсію, ми можемо добути з обох частин наведеного вище співвідношення квадратні корені: стандартне відхилення залишків = 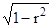(стандартне відхилення у).

(Дисперсія і стандартне відхилення при математичних перетвореннях більш зручні, ніж середні абсолютні відхилення, які ми застосовували на попередніх практикумах).

Значенню у з табл. 3.13 відповідають дисперсія, рівна 50, і стандартне відхилення, рівне 7,1. Ми вже знаємо, що значення коефіцієнта кореляції становить 0,72, отже стандартне відхилення залишків повинно бути таким: 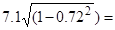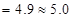. Це досить близько до величини 5,1, одержаної нами безпосередньо за значеннями залишків загалом дисперсія залишків, а також їх стандартне відхилення можуть бути доведені за допомогою коефіцієнта кореляції тільки для відхилень від “регресійного” рівняння, яке буде розглянуто в наступних практикумах. Однак наведений вище метод одержання цих показників може бути застосований на практиці майже для кожного рівняння, котре більше чи менше точно відображає вихідні дані).

“Непояснена варіація” значень у відносно рівняння у = 3х+10, таким чином, менша, ніж варіація самих значень у: стандартне відхилення залишків дорівнює приблизно 5, а значень у – приблизно 7. Однак відмінність між ними незначна. Кореляція повинна бути дуже високою, щоб відмінність між цими показниками була істотною. Ілюстрація цього твердження наведена в табл. 3.14. Співвідношенню, для якого коефіцієнт кореляції дорівнює 0,5, відповідає показник розсіювання залишків, тільки на 13% менший за показник розсіювання для значень у. Але навіть для коефіцієнта кореляції 0,95 ця різниця не перевищує 70 відсотків.

Таблиця 3.14 — Стандартне відхилення залишків, виражене у відсотках стандартного відхилення у

	Коефіцієнт кореляції
0,1	0,3	0,5	0,7	0,9	0,95	0,99

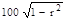
Хоча коефіцієнти кореляції і є мірами розсіву, вони не можуть показати, чи однаковий розкид значень у двох різних сукупностях даних, оскільки при обчисленні кореляції ми знаходимо відношення дисперсії залишків до повної варіації даних, яка для кожного набору спостережень може мати своє власне значення. З рівності двох коефіцієнтів кореляції зовсім не випливає, що і розкид залишків у двох випадків однаковий. Так же само відмінність коефіцієнтів кореляції зовсім не означає, що і розкид залишків у розглянутих сукупностях даних обов’язково має різний характер.

Коефіцієнти кореляції обчислюються для визначення тісноти взаємозв’язку між двома будь-якими характеристиками одного і того ж “об’єкта”. Цей коефіцієнт часто обчислюється для окремої людини, однак його можна знайти, наприклад, і для пар близнят, пляшок вина, адміністративних районів. Сам коефіцієнт кореляції може мати значення від –1,0 до +1,0. Знак коефіцієнта кореляції характеризує напрямок взаємо-зв’язку. Якщо високим значенням однієї змінної відповідають високі значення другої змінної, а низьким значенням – низькі, то кореляція позитивна. Якщо ж високим значенням однієї змінної відповідають низькі значення другої змінної, а низьким значенням – високі, то має місце негативна кореляція. Величина коефіцієнта кореляції (без врахування знака) характеризує ступінь тісноти досліджуваного взаємозв’язку. Сенс цього твердження стане більш зрозумілим після ознайомлення з матеріалом наступного практикуму.

Для прикладу розглянемо вправу “Порівняння двох коефіцієнтів кореляції”. Відомо, що для котроїсь сукупності значень х і у коефіцієнт кореляції дорівнює 0,8.Таке ж значення має коефіцієнт кореляції для другої сукупності значень х і у. Що можна сказати про співвідношення між х і у в цих двох сукупностях даних?

В обох випадках, оскільки кореляція позитивна, більшим значенням х відповідають, як правило, більші значення у. Однак форма зв’язку не обов’язково буде однаковою. Наприклад, у одному випадку співвідношення між х і у може виглядати так: у = 38х + 5, а в другому – у = 0,1х - 10. Величина розкиду фактичних значень навколо теоретичної лінії також може бути різною. Але і від співвідношень і або величина розкиду може виявитись в обох випадках однаковою. Зробити ж будь-який обгрунтований висновок тільки за величиною коефіцієнта кореляції ми просто не спроможні.

Наступна вправа “Два різних коефіцієнта кореляції”. Коефіцієнт кореляції між значеннями росту і ваги котроїсь групи 8-річних дітей дорівнює 0,3, а для групи дітей від 5 до 10 років його величина становить 0,9. Про що свідчить ця різниця?

Невелике значення кореляції для 8-річних дітей можна було б пояснити тим, що розкид їх індивідуальних показників навколо теоретичного рівняння, що пов’язує між собою значення зросту і ваги, значно сильніше, ніж для всієї групи 5-10 річних дітей. Проте відомо, що хлопчики, які належать до вікової групи, що охоплює шість послідовних років (від 5 до 10 років), відрізняються один від одного за зростом і вагою значно більше, ніж хлопчики, які належать до однієї і тієї ж вікової групи. Тому навіть якщо в обидвох випадках буде однаковий розкид залишків, ми можемо очікувати більш високе значення коефіцієнта кореляції для групи 5-10 річних дітей. (Величина кореляції, в кінці, не показує, чи однаковий вид співвідношення між двома змінними в цих двох сукупностях даних).

Поиск по сайту: