Темы рефератов. 1. Советская художественная культура 30-х гг

1. Советская художественная культура 30-х гг.

2. Значение «оттепели» в отечественной культуре.

3. Темы войны в искусстве XX в.

4. Современная НТР и ее влияние на культуру.

5. Роль массовой культуры в жизни современного человека.

6. Влияние средств массовой информации на культуру XX в.

Математический анализ

Вопросы к экзамену – за 2-ой.

II-семестр

1. Понятие первообразной функции и неопределенный интеграл.

2. Свойства неопределенного интеграла.

3. Замена переменных в неопределенных интегралах.

4. Интегрирование по частям.

5. Понятие определенного интеграла. Достаточные условия существования.

6. Свойства определенного интеграла.

7. Теорема о среднем. Формула Ньютона-Лейбница.

8. Замена переменных и интегрирование по частям определенного интеграла.

9. Вычисление площади криволинейной трапеции, объема тела вращения.

10. Понятие функции многих переменных. График функции. Линии уровня.

11. Пределы и непрерывность для функции многих переменных.

12. Частные производные.

13. Дифференциал функции многих переменных.

14. Производная по направлению, градиент.

15. Экстремум функции многих переменных.

16. Дифференциальные уравнения. Теорема о существовании и единственности решения уравнения 1 -го порядка.

17. Системы линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами.

18. Линейные дифференциальные уравнения 2-го порядка. Метод вариации постоянной.

19. Двойной интеграл

20. Вычисление площади плоской фигуры.

21. Вычисление объема тела вращения.

Рекомендуемая литература

Основная литература

Высшая математика для экономистов / Под ред. Н.Ш. Кремера. М, 1998.

Гребенщиков Ю.Б. Математика. Часть 1. Линейная алгебра и основы математического анализа: Учеб. пособие. М., 2002.

Исследование операций в экономике / Под ред. Н.Ш.Кремера. М., 1999.

Красе М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. М., 2001

Дополнительная литература

Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. М., 1982.

Контрольная работа за 2-ый семестр

Вариант 1

1. Вычислите интеграл .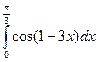

2. Вычислите интеграл .

3. Вычислите интеграл .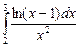

4. Вычислите интеграл .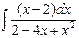

5. Вычислите интеграл .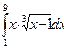

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .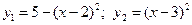

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво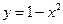й при .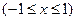

8. Найдите частные производные первого порядка для функции .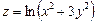

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .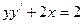

Вариант 2

1. Вычислите интеграл .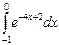

2. Вычислите интеграл .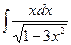

3. Вычислите интеграл .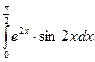

4. Вычислите интеграл .

5. Вычислите интеграл .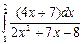

6.Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво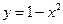й при .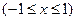

8. Найдите частные производные первого порядка для функции .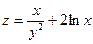

9. Найдите частные производные первого порядка для функции .

10. Решите дифференциальное уравнение .

Вариант 3

1. Вычислите интеграл .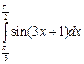

2. Вычислите интеграл .

3. Вычислите интеграл .

4. Вычислите интеграл .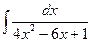

5. Вычислите интеграл .

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .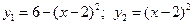

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво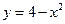й при .

8. Найдите частные производные первого порядка для функции .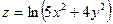

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .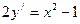

Вариант 4

1. Вычислите интеграл .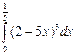

2. Вычислите интеграл .

3. Вычислите интеграл .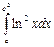

4. Вычислите интеграл .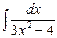

5. Вычислите интеграл .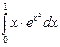

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .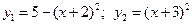

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво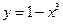й при .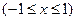

8. Найдите частные производные первого порядка для функции .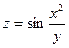

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .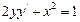

Вариант 5

1. Вычислите интеграл .

2. Вычислите интеграл .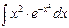

3. Вычислите интеграл .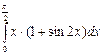

4. Вычислите интеграл .

5. Вычислите интеграл .

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .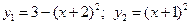

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво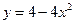й при .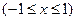

8. Найдите частные производные первого порядка для функции .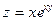

9. Найдите частные производные второго порядка для функции .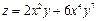

10. Решите дифференциальное уравнение .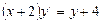

Вариант 6

1. Вычислите интеграл .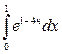

2. Вычислите интеграл .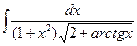

3. Вычислите интеграл .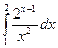

4. Вычислите интеграл .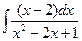

5. Вычислите интеграл .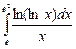

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво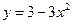й при .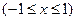

8. Найдите частные производные первого порядка для функции .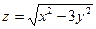

9. Найдите частные производные второго порядка для функции .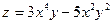

10. Решите дифференциальное уравнение .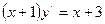

Вариант 7

1. Вычислите интеграл .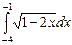

2. Вычислите интеграл .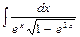

3. Вычислите интеграл .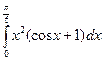

4. Вычислите интеграл .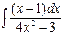

5. Вычислите интеграл .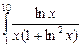

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .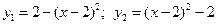

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво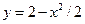й при .

8. Найдите частные производные первого порядка для функции .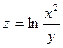

9. Найдите частные производные второго порядка для функции .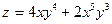

10. Решите дифференциальное уравнение .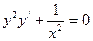

Вариант 8

1. Вычислите интеграл .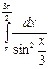

2. Вычислите интеграл .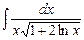

3. Вычислите интеграл .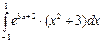

4. Вычислите интеграл .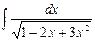

5. Вычислите интеграл .

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .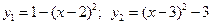

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво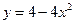й при .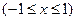

8. Найдите частные производные первого порядка для функции .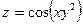

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .

Вариант 9

1. Вычислите интеграл .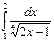

2. Вычислите интеграл .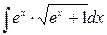

3. Вычислите интеграл .

4. Вычислите интеграл .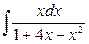

5. Вычислите интеграл .

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .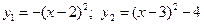

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво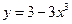й при .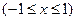

8. Найдите частные производные первого порядка для функции .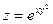

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .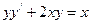

Вариант 10

1. Вычислите интеграл .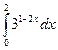

2. Вычислите интеграл .

3. Вычислите интеграл .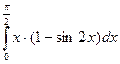

4. Вычислите интеграл .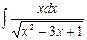

5. Вычислите интеграл .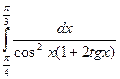

6. Вычислить площадь фигуры, ограниченной графиками функции (между точками их пересечения) .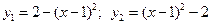

7. Вычислить объем тела, поверхность которого получается при вращении вокруг оси х криво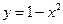й при .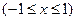

8. Найдите частные производные первого порядка для функции .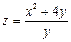

9. Найдите частные производные второго порядка для функции .

10. Решите дифференциальное уравнение .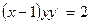

Поиск по сайту: