 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема 9. Линии регрессии. Метод наименьших квадратов ( МНК )
Регрессия одной случайной величины на другую. Регрессия y на x, когда (x, y) имеет двумерное нормальное распределение. Нахождение эмпирической линии регрессии. Определение и основные свойства МНК. МНК для случая линейной сглаживающей функции.
Вопросы для самопроверки
1. Какое событие называется случайным?
2. Какие события называются несовместными?
3. Что такое пространство элементарных событий?
4. Что такое классическая вероятность?
5. Что такое статистическая и геометрическая вероятности?
6. Каковы свойства вероятности?
7. Что такое сумма событий?
8. Что такое произведение событий?
9. Что такое событие, противоположное данному?
10. В чем заключается теорема сложения вероятностей?
11. Что такое условная вероятность?
12. В чем заключается теорема умножения вероятностей?
13. Что такое независимые события?
14. Напишите формулу полной вероятности и формулу Байеса.
15. Напишите формулу Бернулли.
16. Что такое дискретная случайная величина?
17. Что такое непрерывная случайная величина?
18. Что такое закон распределения дискретной случайной величины?
19. Что такое функция распределения случайной величины? Какой вид имеет ее график?
20. Что такое плотность распределения непрерывной случайной величины?
21. Что такое математическое ожидание дискретной и непрерывной случайной величины? Каковы их свойства?
22. Что такое дисперсия и среднее квадратическое отклонение дискретной и непрерывной случайной величины?
23. Каковы свойства дисперсии?
24. Что такое мода, медиана и квантиль?
25. Что такое геометрический закон распределения случайной величины?
26. Что такое закон распределения Бернулли?
27. Что такое распределение Пуассона?
28. Что такое равномерный закон распределения?
29. Что такое экспоненциальный закон распределения?
30. Что такое нормальный закон распределения и каковы его свойства?
31. Что такое случайный вектор?
32. Что такое функция распределения двумерной случайной величины?
33. Что такое ковариация двух случайных величин?
34. В чем заключается закон больших чисел в форме Бернулли?
35. Что такое генеральная совокупность?
36. Что такое вариационный ряд?
37. Что такое эмпирическая функция распределения?
38. Что такое выборочная средняя?
39. Что такое выборочная дисперсия?
40. Какая оценка параметра закона распределения называется несмещенной, а какая состоятельной?
41. Что такое доверительный интервал?
42. Как находится доверительный интервал для математического ожидания нормального распределения при известной дисперсии?
43. Какая гипотеза называется нулевой?
44. Что такое ошибка 1-го рода?
45. Что такое уровень значимости критерия?
46. В чем заключается критерий согласия Пирсона?
47. В чем суть метода наименьших квадратов?
Вопросы к экзамену
1. Основное правило комбинаторики. Перестановки, размещения, сочетания. Бином Ньютона.
2. Классическое определение вероятности события, свойства вероятности.
3. Аксиоматическое, статистическое и геометрическое определение вероятности.
4. Алгебра событий. Теорема сложения вероятностей.
5. Условная вероятность. Теорема умножения вероятностей.
6. Формула полной вероятности. Формула Байеса.
7. Случайные величины. Типы случайных величин. Закон распределения вероятностей дискретной случайной величины.
8. Основные дискретные распределения.
9. Биноминальное распределение; параметры, числовые характеристики.
10. Числовые характеристики дискретных случайных величин, их свойства.
11. Начальные и центральные теоретические моменты.
12. Функция распределения вероятностей одномерной случайной величины (дискретной и непрерывной). Основные свойства функции распределения. Геометрическая интерпретация.
13. Функция плотности распределения вероятностей одномерной случайной величины, свойства функции плотности. Геометрическая интерпретация.
14. Основные числовые характеристики непрерывной случайной величины. Мода, медиана, квантили распределения.
15. Нормальное распределение. Нормированное нормальное распределение. Функция Лапласа. Правило трех сигм.
16. Равномерное распределение.
17. Экспоненциальное распределение.
18. Локальная и интегральная теорема Лапласа.
19. Неравенство Чебышева. Закон больших чисел. Теорема Бернулли. Центральная предельная теорема.
20. Основные понятия математической статистики.
21. Основные выборочные числовые характеристики.
22. Вариационные ряды. Графическое представление вариационного ряда (эмпирическая функция распределения, гистограмма, полигон частот).
23. Понятие оценки параметра, общие требования к оценке параметра.
24. Выборочная оценка математического ожидания, ее свойства.
25. Выборочная оценка дисперсии, ее свойства.
26. Методы получения точечных оценок параметров распределения.
27. Интервальные оценки. Доверительный интервал и доверительная вероятность.
28. Основные распределения, используемые при построении статистических оценок и критериев: нормальное распределение, распределение Пирсона, t-распределение Стьюдента, F-распределение.
29. Доверительный интервал для математического ожидания нормально распределенной случайной величины при известной дисперсии.
30. Доверительный интервал для математического ожидания нормально распределенной случайной величины при неизвестной дисперсии.
31. Доверительный интервал для дисперсии нормально распределенной случайной величины.
32. Статистическая гипотеза. Общая схема проверки гипотезы.
33. Проверка гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии.
34. Проверка гипотезы о числовом значении математического ожидания нормального распределения при неизвестной дисперсии.
35. Проверка гипотезы о равенстве дисперсий двух нормальных распределений.
36. Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений при известных дисперсиях.
37. Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений при неизвестных, но равных дисперсиях.
38. Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события.
39. Сравнение двух вероятностей биноминальных распределений.
40. Критерий согласия χ2 Пирсона.
41. Метод наименьших квадратов.
Варианты контрольных работ
Вариант 1
Даны события:
А = {x: xÎ[3,8]}; B = {x: xÎ[5,7]} Найти: А+В; А-В; АВ; В-А
Известно, что P(A)=0.75, P(AB)=0.5, P(A | B)=0.8.
Найти P(B), P(A + B), P(B | A). Зависимы ли события A и B?
Вероятность того, что лампа остаётся исправной после года работы, равна 0.3. Найти вероятность того, что из четырех ламп после года работы останутся исправными не менее двух.
В группе 30% студентов – отличники, 20% - неуспевающие. Данную задачу отличник решает с вероятностью 0.8, неуспевающий – с вероятностью 0.1, а остальные – с вероятностью 0.6. Студент Петров решил данную задачу. С какой вероятностью этот студент отличник?
5. Слово «МАТЕМАТИКА» разрезали на буквы, 5 из них выложили в ряд. Какова вероятность того, что получится слово «АТАКА»?
6 Из урны, в которой 4 белых шара и 6 черных, вынимают 7 шаров. Найти распределение случайной величины, равной числу оставшихся в урне черных шаров.
7 Плотность распределения вероятности непрерывной случайной величины равна 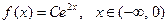 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-2, 2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при известной дисперсии, D = 4, при надежности g = 0,9.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 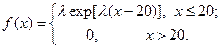
Вариант 2
1. Даны события:
А = {x: xÎ[3,7]}; B = {x: xÎ[5,10]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(B | A)=0.25, P(A)=0.8, P(B)=0.4.
Найти P(A | B), P(A + B), P(AB). Зависимы ли события A и B?
3. Баскетболист бросает мяч в корзину, попадая в 40% случаев. С какой вероятностью из шести бросков окажутся удачными не менее трех?
4. Некоторое изделие выпускается тремя заводами, причем вероятность брака для этих заводов равна 0.2, 0.1 и 0.3 соответственно. Из имеющихся на складе изделий 50% выпущено первым заводом, 30% - вторым, а остальные – третьим. Наугад взятое со склада изделие оказалось бракованным. С какой вероятностью оно было выпущено на втором заводе?
5. Слово «МАКРОЭКОНОМИКА» разрезали на буквы, 7 из них выложили в ряд. Какова вероятность того, что получится слово «МАКРАМЭ»?
6. Из урны, в которой 7 белых шаров и 3 черных наугад вынимают 5 шаров. Найти распределение случайной величины, равной числу оставшихся в урне черных шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна  . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
11. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
12. Найти точечную оценку вероятности попадания в интервал хÎ[-3, 2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
13. Найти несмещенные оценки математического ожидания и дисперсии.
14. Найти интервальную оценку матожидания при неизвестной дисперсии, при надежности g = 0,9.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 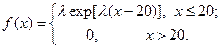
Вариант 3
1. Даны события:
А = {x: xÎ[3,10]}; B = {x: xÎ[5,7]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(AB)=0.2, P(A | B)=0.5, P(B | A)=0.3.
Найти P(A), P(B), P(A + B). Зависимы ли события A и B?
3. В семье четверо детей. Считая, что вероятность рождения мальчика равна 0.4, найти вероятность того, что среди этих детей есть не менее двух мальчиков.
4. В группе 30% студентов – брюнеты, 10% - блондины, а остальные – шатены. За время обучения брюнеты женятся с вероятностью 0.2, блондины – с вероятностью 0.6, а шатены – с вероятностью 0.3. Стало известно, что студент Сидоров женился. С какой вероятностью он блондин?
5. Слово «МИКРОЭКОНОМИКА» разрезали на буквы, 6 из них выложили в ряд. Какова вероятность того, что получится слово «КИМОНО»?
6 Из урны, в которой 4 белых шара и 5 черных, наугад вынимают 3 шара. Найти распределение случайной величины, равной числу вынутых белых шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна 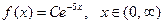 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
15. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
16. Найти точечную оценку вероятности попадания в интервал хÎ[-2, 1], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
17. Найти несмещенные оценки математического ожидания и дисперсии.
18. Найти интервальную оценку дисперсии, при надежности g = 0,9.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 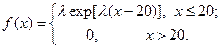
Вариант4
1. Даны события:
А = {x: xÎ(3,8)}; B = {x: xÎ(4,7]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(A)=0.75, P(AB)=0.5, P(A | B)=0.8.
Найти P(B), P(A + B), P(B | A). Зависимы ли события A и B?
3. Вероятность того, что лампа остаётся исправной после года работы, равна 0.3. Найти вероятность того, что из пяти ламп после года работы останутся неисправными не менее двух.
4. В группе 20% студентов – отличники, 10% - неуспевающие. Данную задачу отличник решает с вероятностью 0.9, неуспевающий – с вероятностью 0.1, а остальные – с вероятностью 0.5. Студент Петров решил данную задачу. С какой вероятностью этот студент отличник?
19. Слово «ИНФОРМАТИКА» разрезали на буквы, 5 из них выложили в ряд. Какова вероятность того, что получится слово «КОФТА»?
6. В урне 3 шара с номером 1, 4 шара с номером 2, 5 шаров с номером 3, 4 шара с номером 4. Случайная величина равна номеру вынутого из урны шара. Найти распределения этой случайной величины.
7. Плотность распределения вероятности непрерывной случайной величины равна 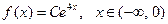 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-4, 2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при известной дисперсии, D = 8, при надежности g = 0,8.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 
Вариант 5
1. Даны события:
А = {x: xÎ[2,4]}; B = {x: xÎ[1,]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(AB)=0.4, P(A + B)=0.8, P(B | A)=0.5.
Найти P(A), P(B), P(A | B). Зависимы ли события A и B?
3. Из партии телевизоров наугад отбирается пять для проверки. Если хотя бы два из проверяемых телевизоров неисправны, то бракуется вся партия. Считая, что каждый телевизор может быть неисправен с вероятностью 0.1, найти вероятность того, что данная партия будет забракована.
4. Среди водителей 10% - робкие, 40% - лихачи, а остальные – солидные. Вероятность попасть в аварию за год для этих водителей составляет 0.3, 0.8 и 0.2 соответственно. Водитель Иванов в прошлом году попал в аварию. Какова вероятность того, что он робкий?
5. Слово «ЛОГИСТИКА» разрезали на буквы, 6 из них выложили в ряд. Какова вероятность того, что получится слово «ЛАСТИК»?
6 Из урны, в которой 4 белых шара и 2 черных, вынимают 3 шара. Найти распределение случайной величины, равной разности чисел вынутых белых и черных шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна 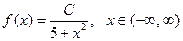 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-3, 4], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при неизвестной дисперсии, при надежности g = 0,8.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 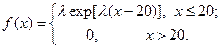
Вариант 6
1. Даны события:
А = {x: xÎ(3,7]}; B = {x: xÎ[6,10)} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(B | A)=0.25, P(A)=0.8, P(B)=0.4. Найти P(A | B), P(A + B), P(AB). Зависимы ли события A и B?
3. Баскетболист бросает мяч в корзину, попадая в 60% случаев. С какой вероятностью из шести бросков окажутся неудачными не менее трех?
4. Некоторое изделие выпускается тремя заводами, причем вероятность брака для этих заводов равна 0.02, 0.01 и 0.03 соответственно. Из имеющихся на складе изделий 40% выпущено первым заводом, 20% - вторым, а остальные – третьим. Наугад взятое со склада изделие оказалось доброкачественным. С какой вероятностью оно было выпущено на втором заводе?
5. Слово «ВЕРОЯТНОСТЬ» разрезали на буквы, 7 из них выложили в ряд. Какова вероятность того, что получится слово «ВЕРНОСТЬ»?
6. Испытание состоит в том, что бросают две монеты. Событие A в одном испытании состоит в выпадении одного орла и одной решки. Найти распределение числа наступления события А в 6 испытаниях.
7. Плотность распределения вероятности непрерывной случайной величины равна 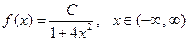 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-6, -2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку дисперсии, при надежности g = 0,8.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 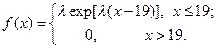
Вариант 7
1. Даны события:
А = {x: xÎ(3,10)} B = {x: xÎ[7,8)} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(AB)=0.2, P(A | B)=0.5, P(B | A)=0.3.
Найти P(A), P(B), P(A + B). Зависимы ли события A и B?
3. В семье пятеро детей. Считая, что вероятность рождения мальчика равна 0.4, найти вероятность того, что среди этих детей есть не менее двух девочек.
4. В группе 30% студентов – брюнеты, 20% - блондины, а остальные – шатены. За время обучения брюнеты женятся с вероятностью 0.02, блондины – с вероятностью 0.06, а шатены – с вероятностью 0.03. Стало известно, что студент Петров женился. С какой вероятностью он шатен?
5. Слово «АРИФМЕТИКА» разрезали на буквы, 5 из них выложили в ряд. Какова вероятность того, что получится слово «ФИРМА»?
6. Из колоды в 36 карт вытаскивают по очереди две (обратно первую не кладут). Пусть пика стоит 1 очко, трефа – 2 очка, бубна – 3 очка, а черва – 4. Случайная величина равна произведению очков на двух картах. Найти распределение этой случайной величины.
7. Плотность распределения вероятности непрерывной случайной величины равна  . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[2, 6], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при известной дисперсии, D = 5, при надежности g = 0,95.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 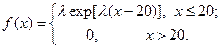
Вариант 8
1.Даны события:
А = {x: xÎ[1,4]}; B = {x: xÎ(1,5]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(AB)=0.4, P(A + B)=0.8, P(B | A)=0.5. Найти P(A), P(B), P(A | B). Зависимы ли события A и B?
3. Из партии телевизоров наугад отбирается пять для проверки. Если хотя бы два из проверяемых телевизоров неисправны, то бракуется вся партия. Считая, что каждый телевизор может быть неисправен с вероятностью 0.2, найти вероятность того, что данная партия будет забракована.
4. Среди водителей 10% - робкие, 50% - лихачи, а остальные – солидные. Вероятность попасть в аварию за год для этих водителей составляет 0.03, 0.06 и 0.02 соответственно. Водитель Попов в прошлом году попал в аварию. Какова вероятность того, что он лихач?
5. Слово «СТЕРЕОМЕТРИЯ» разрезали на буквы, 6 из них выложили в ряд. Какова вероятность того, что получится слово «МЕТЕОР»?
6. Из урны, в которой 4 белых шара и 5 черных, наугад вынимают 3 шара. Найти распределение случайной величины, равной числу вынутых белых шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна  . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-6, 2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при неизвестной дисперсии, при надежности g = 0,95.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 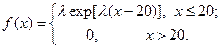
Вариант 9
1 Даны события:
А = {x: xÎ[3,9]} B = {x: xÎ[4,7]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(A)=0.7, P(AB)=0.5, P(A | B)=0.6.
Найти P(B), P(A + B), P(B | A). Зависимы ли события A и B?
3. Вероятность того, что лампа остаётся исправной после года работы, равна 0.4. Найти вероятность того, что из четырех ламп после года работы останутся исправными не менее двух.
4. В группе 20% студентов – отличники, 30% - неуспевающие. Данную задачу отличник решает с вероятностью 0.8, неуспевающий – с вероятностью 0.1, а остальные – с вероятностью 0.5. Студент Петров решил данную задачу. С какой вероятностью этот студент отличник?
5. Слово «МАТЕМАТИКА» разрезали на буквы, 5 из них выложили в ряд. Какова вероятность того, что получится слово «АТАКА»?
6. Из урны, в которой 4 белых шара и 8 черных, вынимают 9 шаров. Найти распределение случайной величины, равной числу оставшихся в урне черных шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна 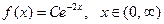 . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
8. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
9. Найти точечную оценку вероятности попадания в интервал хÎ[-2, 5], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
10. Найти несмещенные оценки математического ожидания и дисперсии.
11. Найти интервальную оценку дисперсии, при надежности g = 0,95.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 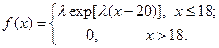
Вариант10
1. Даны события:
А = {x: xÎ[1,7]} B = {x: xÎ[5,10]} Найти: А+В; А-В; АВ; В-А
2. Известно, что P(B | A)=0.25, P(A)=0.7, P(B)=0.4.
Найти P(A | B), P(A + B), P(AB). Зависимы ли события A и B?
3. Баскетболист бросает мяч в корзину, попадая в 55% случаев. С какой вероятностью из шести бросков окажутся удачными не менее трех?
4. Некоторое изделие выпускается тремя заводами, причем вероятность брака для этих заводов равна 0.25, 0.15 и 0.3 соответственно. Из имеющихся на складе изделий 50% выпущено первым заводом, 30% - вторым, а остальные – третьим. Наугад взятое со склада изделие оказалось бракованным. С какой вероятностью оно было выпущено на втором заводе?
5. Слово «МАКРОЭКОНОМИКА» разрезали на буквы, 7 из них выложили в ряд. Какова вероятность того, что получится слово «МАКРАМЭ»?
6. Из урны, в которой 8 белых шаров и 3 черных наугад вынимают 5 шаров. Найти распределение случайной величины, равной числу оставшихся в урне черных шаров.
7. Плотность распределения вероятности непрерывной случайной величины равна  . Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
. Найти нормировочный множитель С, математическое ожидание М(Х) и дисперсию D(X).
Дан вариационный ряд для непрерывной случайной величины.
| [Dxi] | [-7, -5] | [-5, -3] | [-3, -1] | [-1, 1] | [1, 3] | [3, 5] | [5, 7] |
| ni |
1. Построить гистограмму приведенных относительных частот и соответствующую эмпирическую функцию распределения.
2. Найти точечную оценку вероятности попадания в интервал хÎ[-6, 2], полагая, что величина Х равномерно распределена внутри каждого интервала группировки.
3. Найти несмещенные оценки математического ожидания и дисперсии.
4. Найти интервальную оценку матожидания при известной дисперсии, D = 9, при надежности g = 0,98.
12. Методом максимального правдоподобия найти точечную оценку параметра λ по данной выборке
| Х | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | 13-15 | 15-17 | 17-19 |
| n |
при условии, что соответствующая непрерывная случайная величина имеет плотностью распределения 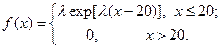
Рекомендуемая литература
Основная литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. «ВЫСШАЯ ШКОЛА», М., 1998.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. «ВЫСШАЯ ШКОЛА», М., 1998.
3. Криволапов С.Я. Теория вероятностей: Учеб. пособие по курсу «Высшая математика». ВГНА МНС России, М., 1999.
4. Криволапов С.Я. Математическая статистика: Учеб. пособие по курсу «Высшая математика». ВГНА МНС России, М., 2000.
Дополнительная литература
1. Глебов В.И. и др. Задачи по теории вероятностей (с решениями): Учебное пособие. М., ВГНА МНС России 2003.
2. Карасев А.И. Теория вероятностей и математическая статистика. ВГНА МНС России, М., 1979.
3. Криволапов С.Я. Сборник задач по математической статистике: Учебное пособие. ВГНА МНС России, М., 2004.
Поиск по сайту: