Формы выражения теплоемкости

Из уравнения первого начала после его дифференцирования по температуре следует:

, (2.1)

где и называется истинной теплоемкостью.

Истинная теплоемкость показывает, какое количество теплоты следует подвести к системе для заданного повышения ее температуры.

Часто, особенно при решении практических задач, пользуются величиной средней теплоемкости:

, (2.2)

где - средняя теплоемкость;

- изменение температуры системы.

В зависимости от того, к какому количеству (массе) вещества относится рассматриваемая теплоемкость, различают:

а) удельную теплоемкость, определяющую то количество теплоты, которое необходимо сообщить системе массой 1 кг для ее нагрева в заданном температурном интервале, Дж/кг К;

б) молярную теплоемкость, характеризующую то количество теплоты, которое необходимо сообщить системе с количеством вещества 1 моль, для ее нагрева в заданном температурном интервале, Дж/моль К.

Функция q не является функцией состояния, поэтому и теплоемкость так же зависима от условий совершения процесса теплопередачи.

В этой связи различают изобарическую (С_Р) и изохорическую (С_V) теплоемкости.

Из уравнения (2.1) следует, что для условий V = const (изохорический процесс) справедливо следующее:

, (2.3)

где dV = 0, поэтому:

. (2.4)

Для изобарических условий ведения процесса (р = const):

. (2.5)

Сравним С_V и С_Р:

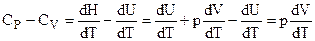. (2.6)

Из уравнения состояния идеального газа:

. (2.7)

Тогда (2.6) с учетом (2.7) запишется в виде (2.8):

,

т. е.

С_Р - С_V = R. (2.8)

Соотношение (2.8) называется формулой Майера для идеальных газов.

Для твердых веществ различие между С_Р и С_V невелико, а их взаимозависимость описывается более сложным соотношением:

, (2.9)

где Т - температура;

- изобарический коэффициент линейного расширения;

- изотермический коэффициент сжатия;

V ₀ - молярный объем вещества при 0 К.

Поиск по сайту: