Химический потенциал

Если в качестве экстенсивного свойства выбирается энергия Гиббса раствора (G), то ее величина, в отличие от значения G для идеального газа (4.67), зависит еще и от чисел молей компонентов раствора:

G = f (P, T, n₁, n₂,...). (7.33)

Согласно (7.25) парциальная мольная энергия i-го компонента раствора вычислится:

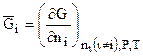. (7.34)

Величина названа Дж. У. Гиббсом химическим потенциалом i-го компонента смеси, обозначаемая как .

После введения (7.34) в (7.26):

. (7.35)

В состоянии термодинамического равновесия dG = 0, поэтому условие термодинамического равновесия в гетерогенной системе при Р = const и Т = const запишется в виде:

. (7.36)

Химический потенциал - интенсивная характеристика компонента раствора и, согласно (7.36), условием равновесия системы является равенство в различных ее частях.

Практически важно, таким образом, уметь рассчитывать значения для различных систем.

1. Система “идеальный газ”.

Известно (4.67), что dG = Vdp - SdT. В изотермических условиях dG = Vdp, где 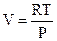. Поэтому: . Для Р = 1 (стандартные условия) const = G⁰. Окончательно:

G = G⁰ + RTlnP. (7.37)

Но в идеальных системах парциальные молярные характеристики совпадают с молярными, поэтому, считая насыщенный пар идеальным газом, окончательно:

, (7.38)

где 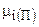- химический потенциал i-го компонента, находящегося в газообразном состоянии;

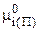- то же, но в стандартных условиях;

Р_i - парциальное давление i-го компонента газовой смеси (насыщенного пара).

2. Система “чистая жидкость - насыщенный пар”.

Так как система находится в состоянии термодинамического равновесия, то

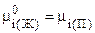, (7.39)

где - химический потенциал чистого вещества в жидком состоянии.

С учетом (7.38):

, (7.40)

где - парциальное давление насыщенного пара над чистой жидкостью.

3. Система “раствор - насыщенный пар”.

Система находится в состоянии термодинамического равновесия, поэтому имеет место равенство:

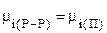, (7.41)

где 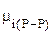- химический потенциал i-го компонента в растворе.

С учетом (7.38):

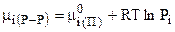, (7.42)

где

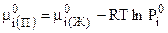. (7.43)

Тогда (7.42) после замены 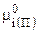из (7.43) примет вид:

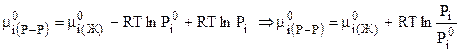. (7.44)

Если поведение i-го компонента описывается законом Рауля, то:

, (7.45)

где N_i - мольная доля i-го компонента раствора.

Для системы “разбавленный раствор - пар” в состоянии теромодинамического равновесия:

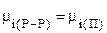
и с учетом (7.38)

,

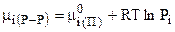где Р_i = Г N_i.

Тогда:

, (7.46)

где 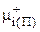- химический потенциал i-го компонента в гипотетическом состоянии.

Гипотетическое (надуманное) состояние достигается экстраполяцией закона Генри до N_i=1, при условии, что раствор остается разбавленным.

Поиск по сайту: