Термодинамический взгляд на энтропию

Подвод энергии к системе способом теплопередачи приводит к повышению уровня беспорядочного движения частиц в системе. Из этого следует, что при нагревании системы можно ожидать увеличения энтропии. Но записать dS = dq неоправдано по двум причинам: энтропия - функция состояния, а теплота таковой не является. С другой стороны, переход энергии к системе способом теплопередачи вызывает больший хаос в более холодной системе, чем такой же - в горячей.

Простейшее предположение состоит в том, что затраты энергии на разупорядочение в системе dq обратно пропорциональны Т.

Поэтому с термодинамической точки зрения энтропия - нечто, изменяющееся следующим образом:

, (4.21)

где Т - характеристика уже существующей разупорядоченности в системе;

dq_обр - величина разупорядочивающего влияния.

Индекс “обр.” указывает, что теплопередача организавана в обратимом режиме.

Соотношение может быть получено из анализа работы тепловой машины, работающей в режиме произвольного цикла, состоящего из обратимых процессов (рис. 4.5).

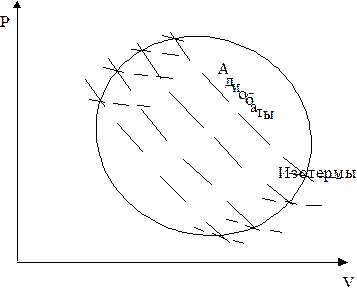
Если этот контур разбить большим числом адиабат, а через точки пересечения адиабат с контуром провести изотермы, то получаются бесконечно малые циклы Карно. Площади этих циклов при достаточной близости адиабат друг к другу мало отличаются по площади от циклов, ограниченных адиабатами и контуром цикла.

Из теоремы Карно для случая обратимого цикла следует:

, (4.22)

или

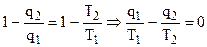, (4.23)

Для каждого из бесконечно малых циклов согласно (4.23) справедливы равенства:

- для ‘ цикла;

- для “ цикла и т. д. (4.24)

Суммирование равенств (4.24) дает:

, (4.25)

где - приведенная теплота.

Тогда соотношение (4.25) может быть записано в виде:

, (4.26)

т.е. алгебраическая сумма приведенных теплот равна нулю.

В пределе эта сумма переходит в интеграл, взятый по замкнутому контуру (равенство Клазиуса):

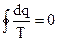, (4.27)

Так как интеграл по контуру от некоторой функции равен нулю, то подинтегральное выражение - полный дифференциал, а сама функция есть функция состояния. Эта функция названа энтропией (S).

Следовательно:

, (4.28)

и

, (4.29)

Соотношения (4.28) и (4.29) - математические выражения второго начала термодинамики, причем (4.29) справедливо только для обратимого режима ведения процесса.

При рассмотрении необратимого цикла, справедливо неравенство:

, (4.30)

тогда

или

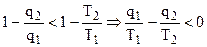, (4.31)

т. е. алгебраическая сумма приведенных теплот меньше нуля.

По аналогии с вышеизложенными:

и , (4.32)

что соответствует неравенству:

(4.33)

или

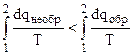, (4.34)

где

. (4.35)

После дифференцирования (4.34) окончательно:

. (4.36)

Неравенство (4.36) представляет математическую форму второго закона термодинамики для необратимых процессов.

После обобщения (4.27) и (4.32) математическая форма записи второго закона термодинамики имеет вид:

(4.37)

или в дифференциальной форме записи:

, (4.38)

где знак неравенства относится к необратимым, а знак равенства - к обратимым процессам.

Поиск по сайту: