Уравнение Гиббса - Гельмгольца

Функции F и G, как оказалось - надежный критерий оценки возможности, направления и пределов протекания естественных процессов в неизолированных системах. Однако при решении реальных задач возникает необходимость знания зависимости F и G от температуры.

После дифференцирования (4.57):

dF = dU - TdS - SdT,

где TdS = dU + pdV.

Тогда:

dF = dU - dU - pdV - SdT = -pdV - SdT,

из чего:

F = f (V, T). (4.64)

Тогда:

, (4.65)

где

= -p, а = -S. (4.66)

Аналогично:

dG = dU + pdV + Vdp - TdS - SdT,

где TdS = dU + pdV.

Тогда:

dG = dU + pdV + Vdp - dU - pdV - SdT = Vdp - SdT,

следовательно

G = f (p, T). (4.67)

После дифференцирования (4.67):

,

откуда

, а , (4.68)

После замены из (4.66) и (4.68) уравнения (4.57) примут вид:

и . (4.69)

Получены два важных уравнения, называемые уравнениями Гиббса - Гельмгольца, устанавливающие зависимость F и G, при V и p = const соответственно, от температуры.

Составляя уравнения (4.69) для исходного и конечного состояния системы и вычитая первые из вторых можно получить соотношения для изменения этих функций:

и . (4.70)

Из ранее изложенного:

; ; ; .

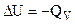Поэтому:

, a (4.71)

или уравнение Гиббса - Гельмгольца в обобщенной форме записи:

, (4.72)

где - температурный коэффициент работы.

Поиск по сайту: