 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Энергия активации
Опытные данные свидетельствуют о том, что скорость химической реакции быстро растет с повышением температуры.
Существует эмпирическое правило Вант - Гоффа, согласно которому повышение температуры на 10 К увеличивает скорость реакции в 2 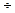 4 раза. В аналитической форме записи:
4 раза. В аналитической форме записи:
 , (10.22)
, (10.22)
где  и
и  - константы скоростей реакции при Т1 и Т2 соответственно;
- константы скоростей реакции при Т1 и Т2 соответственно;
 .
.
В соответствии с этим правилом изменение температуры на 100 К приведет к увеличению скорости реакции в 310 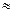 60 тыс. раз.
60 тыс. раз.
Правило Вант - Гоффа не выполняется при высоких температурах.
Примером быстрого роста скорости реакции с температурой могут служить данные табл. 10.1 для реакции разложения иодистого водорода. В последнем столбце приведено время полураспада  при начальной концентрации HI в 1 моль/л.
при начальной концентрации HI в 1 моль/л.
Таблица 10.1. Константа скорости и период полураспада реакции 2HI = H2 + I.
| t, 0C | T, K | kНАБЛ. 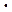 105 105
| kВЫЧ. 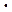 105 105
| 
|
| - | 1,0 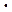 10-10 10-10
| 314000 лет | ||
| - | 0,000029 | 109 лет | ||
| 0,0352 | 0,0315 | 34 дня | ||
| 3,02 | 3,25 | 9,3 час. | ||
| 22,0 | 23,8 | 1,3 час. | ||
| 14 мин. | ||||
| 25 сек. | ||||
| - | 1,6 сек. | |||
| - | 0,12 сек. |
Более точная зависимость скорости реакции от температуры выражается уравнением Аррениуса (1889 г.), устанавливающим увеличение константы скорости реакции с ростом температуры:
 , (10.23)
, (10.23)
где Е - энергия активации химической реакции.
Физический смысл Е объясняется на основе теоретических представлений химической кинетики и будет рассмотрен ниже. Уравнение Аррениуса достаточно хорошо выполняется как для простых гомогенных, так и для многих гетерогенных реакций. Отклонение от этого уравнения указывает на сложность механизма течения реакции.
Уравнение (10.23) может быть записано как для прямой, так и для обратной реакции с энергиями активации Е1 и Е2 соответственно:
 и
и  .
.
Вычтем из первого уравнения второе:
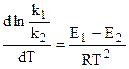 ,
,
где  .
.
Из уравнения изохоры химической реакции (4.96) следует, что 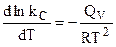 , поэтому окончательно:
, поэтому окончательно:
Е1 - Е2 = -QV. (10.24)
Таким образом, разность энергий активации прямой и обратной реакций численно равна ее тепловому эффекту.
Аналогичным образом можно рассмотреть реакцию, протекающую в условиях р = const. В этом случае следует пользоваться уравнением изобары и связывать разность энергий активации прямого и обратного процесса с  .
.
Изменение энергии системы, в которой происходит химическое взаимодействие представлено на рис.10.2.

|
Уровень I соответствует исходным продуктам, уровень II - конечным продуктам реакции. Как видно из рисунка, энергия системы вначале возрастает до уровня k, а затем уменьшается до уровня II - в ходе реакции преодолевается энергетический барьер. Величина этого барьера характеризует ту минимальную дополнительную энергию Е1 по сравнению со средней энергией теплового движения U1, которую нужно сообщить исходным продуктам для того, чтобы произошла реакция. Эта величина называется энергией активации.
| Рис. 10.2. Изменение энергии системы в ходе химической реакции. |
При протекании реакции в обратном направлении энергия активации равна Е2. Именно такую дополнительную энергию должна приобрести система, находящаяся на уровне II, для преодоления энергетического барьера. После этого образуются вещества, энергия теплового движения которых отвечает уровню I.
Представление об энергетическом барьере предполагает, что молекулы реагентов не всегда могут вступать в реакцию. Таким молекулам недостаточно просто встретиться. Они должны столкнуться, обладая достаточно высокими скоростями относительного движения. За счет кинетической энергии этого движения и преодолевается энергетический барьер. Дополнительная энергия может быть получена молекулами реагентов, например, за счет поглощения энергии излучения.
Существование реакций, с резко отличающимися друг от друга величинами энергий активации объясняет и различия в скоростях их протекания: в случае очень большой энергии активации будет очень мало молекул, способных преодолевать энергетический барьер. и скорость реакции должна быть незначительной. Подсчеты показывают, что если все столкновения молекул были бы активными, то реакция имела бы взрывной характер.
Наконец, сильная температурная зависимость скорости химической реакции тоже объясняется лишь в предположении о более эффективном взаимодействии активных молекул, так как общее число столкновений незначительно увеличивается с ростом температуры.
Уравнение Аррениуса можно представить в интегральной форме записи:

после интегрирования:
 ,
,
если Е  f (Т).
f (Т).
Полученное уравнение в координатах  выражается прямой, тангенс угла наклона которой к оси абсцисс есть величина
выражается прямой, тангенс угла наклона которой к оси абсцисс есть величина  .
.
Если  , что справедливо для
, что справедливо для  ,
,  , поэтому:
, поэтому:
 , (10.25)
, (10.25)
и окончательно
 , (10.26)
, (10.26)
где  - частотный фактор.
- частотный фактор.
Поиск по сайту: