Следствия из тепловой теоремы Нернста

I следствие. Производная в соответствии с уравнением Кирхгофа (3.26) равна алгебраической сумме теплоемкостей составных частей системы. Но , поэтому:

. (5.9)

Это означает, что при абсолютном нуле для конденсированных систем строго соблюдается правило Неймана - Коппа об аддитивности теплоемкостей.

Нернст пошел дальше и доказал, что не только алгебраическая сумма всех теплоемкостей равна нулю (5.9), но и теплоемкость каждого в отдельности конденсированного тела равна нулю:

. (5.10)

Ранее в главе II показано, что этот вывод находится в согласии с опытом и что он следует из квантовой теории теплоемкости.

II следствие. Согласно тепловой теории Нернста 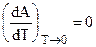. Но , a 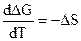, поэтому:

. (5.11)

Условие (5.11) показывает, что при любых процессах с конденсированными телами при абсолютном нуле температуры энтропия не изменяется. Это равносильно тому, что энтропии всех конденсированных тел при Т 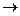0 одинаковы. М. Планк (1912 г.), расширяя теорему Нернста, предложил, что и для каждого конденсированного тела в отдельности:

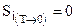, (5.12)

т. е. энтропия правильно образованного кристалла чистого вещества при абсолютном нуле температур равна нулю.

Формулировка М. Планка позволяет вычислять абсолютные значения энтропии, что открыло путь к широкому применению таблиц термодинамических функций для вычисления химических равновесий.

III следствие. Для того, чтобы найти величину const в уравнении (5.4) можно поступить следующим образом: уравнение 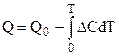вводится в уравнение (5.3):

.

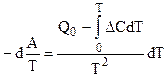Интегрирование в пределах от 0 до Т дает:

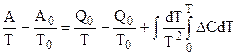
или

.

Полученное выражение идентично выражению (5.4), если положить, что . Но согласно уравнению Гиббса - Гельмгольца ():

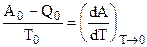, где .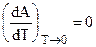

Поэтому:

const = 0, (5.13)

что устраняет неопределенность в интеграле уравнения Гиббса - Гельмгольца (5.4) и позволяет получить истинные значения А = f (Т) для конденсированных систем.

Теорема Нернста непосредственно к газовым равновесиям неприменима. Поэтому для них она не может дать численного значения const в уравнении Гиббса - Гельмгольца (5.4).

Однако косвенным путем она дает важные сведения. Оказывается, что величина const интегрирования в уравнении изобары химической реакции:

равна алгебраической сумме истинных химических постоянных продуктов химической реакци:

, (5.14)

что позволяет вычислять химическое сродство при различных температурах для газовых равновесий.

Поиск по сайту: