Температурная зависимость теплоемкости

Теплоемкость изменяется с изменением температуры, причем величина этого изменения различна в различных температурных интервалах.

Качественно характер изменения С = f (Т) для большинства металлов, не испытывающих фазовых превращений в твердом состоянии представлен на рис. 2.1.

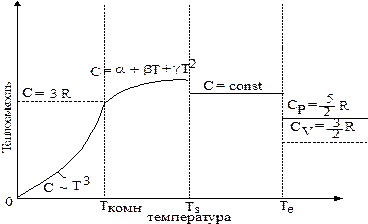
Рис. 2.1. Характер изменения теплоемкости с температурой.

Для металлов в твердом состоянии в области низких температур (T < T_комн.) характерна зависимость отвечающая уравнению кубической параболы: 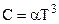. С понижением температуры теплоемкость быстро уменьшается и при 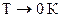стремится принять нулевое значение. В области комнатных температур (Т_комн.) теплоемкость определяется из закона Дюлонга - Пти. Дальнейшее повышение температуры плавления (Т_S) вызывает непрерывное увеличение теплоемкости. Этот температурный участок представляет наибольший практический интерес. Для него зависимость С = f (Т) выражается с помощью эмпирических соотношений, имеющих вид степенных рядов:

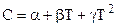, (2.18)

, (2.19)

Теплоемкость для жидкого состояния (Т_S - T_E) характеризуется, как правило, меньшей величиной, чем для твердого состояния, причем не изменяющейся вплоть до температуры кипения (Т_Е).

Так как большинство металлов в газообразном состоянии - одноатомные газы, то их теплоемкости определяются из закона Дюлонга - Пти.

6. Квантовая теория теплоемкости

Квантовая теория теплоемкости возникла с потребностью объяснения наблюдаемой экспериментально зависимостью C = f (T), которая не соответствовала теоретическим представлениям, вытекающим из правила Дюлонга – Пти.

Первоначально созданная теория теплоемкости Эйнштейна лишь качественно объяснила уменьшение теплоемкости при Т 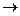0 К; наблюдаемое уменьшение не было таким стремительным.

Теория теплоемкости Дебая возникла в связи с тем, что в первоначальную теорию Эйнштейна были введены чрезмерные упрощения:

- все 3N_A колебаний имеют одну и ту же частоту;

- каждый атом – независимая вибрирующая частица, испытывающая гармонические колебания около фиксированной точки – узла кристаллической решетки.

Основные положения квантовой теории теплоемкости Дебая состоят в следующем:

1) имеется целый спектр частот колебаний атомов от 0 до V _MAX, причем частота колебаний может принимать лишь дискретные значения. Колебания данного атома влияют на поведение соседей;

2) средняя энергия одного типа колебаний равна:

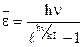, (2.20)

где h – постоянная Планка, равная 6,625 * 10^-34 Дж * с;

3) полная энергия колебательного движения решетки рассчитывается путем суммирования энер-

гий всех типов колебаний атомов:

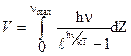, (2.21)

где Z = f (V).

Окончательно:

, (2.22)

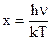где , а .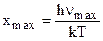

Если 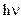<< kT (область высоких температур), то U = 3RT, а 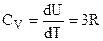, что согласуется с классической теорией теплоемкости Дюлонга – Пти.

Если 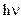>> kT (область низких температур), то 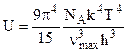, а 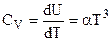- известная из эксперимента параболическая зависимость.

Величина , где - характеристическая температура. Ее физический смысл состоит в том, что при Т < необходимо учитывать квантово – механические эффекты, в противном случае они не проявляются и теплоемкость определяется на основе классической теории теплоемкости.

Характеристическая температура рассчитывается:

, (2.23)

где а – параметр кристаллической решетки;

Е – модуль упругости;

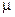- молярная масса.

Значения характеристической температуры для ряда веществ приведены в таблице 2.1.

Таблица 2.1. Характеристические температуры.

Поиск по сайту: