Уравнение правила фаз

Пусть рассматриваемая система состоит из f - фаз и k - компонентов, причем каждый из k - компонентов находится в каком-то количестве в каждой из f - фаз.

Давление и температура одинаковы для всех фаз данной системы, т.е. имеется два общих параметра состояния.

Так как каждый компонент находится в каждой фазе, то возможные концентрации компонентов во всех фазах:

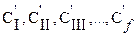- для первого компонента;

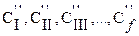- для второго компонента;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- для k - го компонента. (6.1)

Число возможных концентраций компонентов составит величину k 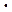f. Итого, для рассматриваемой системы общее число параметров состояния равно (k 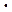f + 2), где цифра учитывает число общих параметров для всех фаз данной системы - давление и температуру.

Для каждой из фаз имеется свое уравнение состояния.

Например, для первой фазы это уравнение таково:

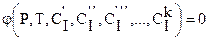. (6.2)

Таких уравнений столько, сколько фаз в системе, т.е. f - штук.

Система находится в состоянии термодинамического равновесия, что означает равенство химических потенциалов компонентов (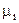) во всех фазах системы, т.е.:

- для первого компонента;

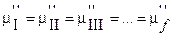- для второго компонента;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- для k - го компонента. (6.3)

Число строк в матрице равно числу компонентов (k), а число столбцов равно (f - 1), тогда общее число уравнений составит:

k(f - 1).

Таким образом, общее число уравнений, связывающих значения химических потенциалов компонентов вычислится как

f + k(f - 1).

Согласно определению, число степеней свободы равно разности между общим числом параметров состояния и числом уравнений, связывающих эти параметры:

с = (k 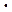f + 2) - [ f + k(f - 1)]

или

с = k - f + 2. (6.4)

т. е. число степеней свободы равно разности между числом компонентов и фаз плюс два.

В системах без участия в равновесии газообразной фазы, один из параметров, общий для всех фаз системы, а именно давление, не оказывает влияние на равновесие в системе, если изменяется в небольших пределах и поэтому исключается из числа общих параметров состояния. Это положение применимо, в частности, к металлическим расплавам и поэтому уравнение правила фаз записывается в виде:

с = k - f + 1. (6.5)

Равновесие нонвариантно (безвариантно), если с = 0, моновариантно (одновариантно), если с = 1 и дивариантно (двухвариантно), если с = 2.

Поиск по сайту: