ОСНОВНЫЕ ФОРМУЛЫ. · Формула Эйнштейна для фотоэффекта

· Формула Эйнштейна для фотоэффекта

где hn - энергия фотона, падающего на поверхность металла; А – работа выхода электрона; Т – кинетическая энергия фотоэлектрона.

· Красная граница фотоэффекта:

n₀=A/h или l₀ = hc/A,

где n₀ – минимальная частота света, при которой еще возможен фотоэффект; l₀ – максимальная длина волны света, при которй еще возможен фотоэффект; h – постоянная Планка; с – скорость света в вакууме.· Формула Комптона:

или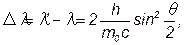

где l - длина волны фотона, встретившегося со свободным или слабо связанным электроном; l^’ длина волны фотона, рассеянного на угол q после столкновения с электроном: m₀ – масса покоящегося электрона.

· Комптоновская длина волны для электрона:

· Давление света при нормальном падении на поверхность:

где Е – облученность поверхности или плотность потока энергии; w - объемная плотность лучистой энергии; r - коэффициент отражения света поверхностью.

· Длина волны де Бройля: l = 2p /p, где р – импульс частицы.

· Релятивистская масса:

где m₀ – масса покоя частицы; u - ее скорость; с – скорость света в вакууме; b - скорость частицы, выраженная в долях скорости света (b = u/с).

· Импульс частицы:

а) в нерелятивистском случае:

p = m₀u,

б) в релятивистском случае:

где m₀ - масса покоя частиц; m – релятивистская масса; u - скорость частицы; с – скорость распространения электромагнитного излучения в вакууме.

· Взаимосвязь массы и энергии релятивистской частицы:

где Е₀ = m₀c² – ‘энергия покоя частицы.

· Полная энергия свободной частицы:

Е = Е₀ + Т,

где Т – кинетическая энергия релятивистской частицы.

· Кинетическая энергия релятивистской частицы:

· Связь импульса частицы с кинетической энергией Т:

а) в нерелятивистском случае

б) в релятивистском виде:

где Е₀ – энергия покоя частицы (Е₀ = m₀c²).

· Связь между полной энергией и импульсом релятивистской частицы::

Е² = Е₀²+ (рс)².

· Соотношение неопределенностей

а) для координаты и импульса

Dр_хDх ³ ,

где Dр_х – неопределенность проекции импульса на ось х; Dх – определенность координаты;

б) для энергии и времени DЕDt³ ,

где DЕ – неопределенность энергии; Dt – время жизни квантовой системы в ином энергетическом состоянии.

· Одномерное уравнение Шредингера для стационарных состояний:

где y(х) – волновая функция, описывающая состояние частицы; m – масса частицы; Е – полная энергия; U = U(x) - потенциальная энергия частицы.

· Плотность вероятности:

где dw(x) – вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dx.

· Вероятность обнаружения частицы в интервале значений от х₁ до х₂:

· Решение уравнения Шредингера для одномерного, бесконечно глубокого прямоугольного потенциального ящика:

а) собственная нормированная волновая функция

б) собственное значение энергии

где n – квантовое число (n = 1,2,3,…); l – ширина ящика. В области 0 £ х, x ≥ ℓ, U = ¥ и (х) = 0.

· Момент импульса электрона (второй постулат Бора):

где m – масса электрона; u_n – скорость электрона на n-ной орбите; r_n – радиус n-ной орбиты (дозволенной); - постоянная Планка ( =1,05^.10^-34 Дж^.м); n = 0 не реализуется).

· Радиус боровской орбиты:

r_n = a₀n²,

где a₀ = 52,9 пм – радиус боровской орбиты.

· Энергия электрона в атоме водорода:

Е_n = -E_i/n²,

где Е_i = 13,6 эВ – энергия ионизации водорода.

· Энергия, излучаемая или поглощаемая атомом водорода:

e

или

где n₁ и n₂ – квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме.

· Спектроскопическое волновое число:

где l - длина волны излучения или поглощения атомом; R = 1,097^.10⁷ м^-1 – постоянная Ридберга.

· Массовое число ядра (число нуклонов в ядре)

А = Z + N,

где Z – зарядовое число (число протонов), N – число нейтронов.

· Основной закон радиоактивного распада:

N = N₀ e^{-l t}

где N – число ядер, не распавшихся к моменту времени t; N₀ – число ядер в начальный момент времени (t=0); l - постоянная радиоактивного распада.

· Число ядер, распавшихся за время t:

DN = N₀ – N = N₀(I-e^-lt)

В случае, если промежуток времени Dt, за который определяется число распавшихся ядер, много меньше периода полураспада Т_1/2, то число распавшихся ядер можно определить по формуле

DN = lNDt.

· Зависимость периода полураспада от постоянной радиоактивного распада:

Т_1/2 = In2/l = 0,693/l.

· Cреднее время жизни t радиоактивного ядра, т.е. промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:

t = I/l.

· Число N атомов, содержащихся в радиоактивном изотопе

гдн m – масса изотопа; m - молярная масса; N_A – число Авогадро.

· Активность А радиоактивного изотопа:

или

где dN – число ядер, распадающихся за интервал времени dt; А₀ – активность изотопа в начальный момент времени.

· Удельная активность изотопа:

а = А/m

· Дефект массы ядра:

Dm = Zm_p+(A-Z)m_n-m_я,

где Z – зарядовое число (число протонов в ядре); А – массовое число (число нуклонов в ядре); (A-Z) – число нейтронов в ядре; m_p – масса протона; m_n – масса нейтрона; m_я – масса ядра.

· Энергия связи ядра:

Е_св = Dmc²,

где Dm – дефект массы ядра; c- скорость света в вакууме.

Во внесистемных единицах энергия связи ядра равна

Е_св = 931Dm,

где Dm – дефект массы в а.е.м.; 931 – коэффициент пропорциональности (1 а.е.м. ~931 МэВ).

· Молярный объем кристалла:

V_m = m/r,

где m - молярная масса; r - плотность кристалла.

· Объем элементарной ячейки в случае решетки кубической сингонии:

V_эл = а³,

где а – параметр решетки.

· Число элементарных ячеек в одном моле кристалла

Z_m = V_m/V_эл,

если кристалл состоит из одинаковых атомов, то

Z_m = N_A/n

где n – число одинаковых атомов, приходящихся на элементарную ячейку; N_A – число Авогадро.

· Число элементарных ячеек в единице объема кристалла:

если кристалл состоит из одинаковых атомов, то

· Параметр кубической решетки, состоящей из одинаковых атомов:

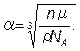
· Расстояние между соседними атомами в кубической решетке:

а) в гранецентрированной

d = a/

б) в объемно-центрированной

.

· Среднее значение энергии квантового одномерного осциллятора:

,

где e₀ нулевая энергия (e₀= ; - постоянная Планка; w - циклическая частота колебаний осциллятора; k – постоянная Больцмана; Т – термодинамическая температура.

· Молярная внутренняя энергия системы, состоящей из невзаимодействующих квантовых осцилляторов:

где R – универсальная газовая постоянная; q _Е - характеристическая температура Эйнштейна (q _Е = ) U₀ – молярная нулевая энергия (по Эйнштейну)

· Молярная теплоемкость кристаллического твердого тела по Дебаю:

где q_D – характеристическая температура Дебая .

· Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая):

Эта формула справедлива при условии T<<q_D.

· Теплота, необходимая для нагревания тела:

где m – масса тела; m - молярная масса; Т₁ и Т₂ – начальная и конечная температуры тела.

· Распределение свободных электронов в металле по энергиям при абсолютном нуле:

,

где dn(e) - концентрация электронов, энергии которых заключены в пределах от e до e +de, m – масса электрона.

Это выражение справедливо при e<e_f (где e_f – энергия или уровень Ферми).

· Энергия Ферми в металле при Т = 0:

где n – концентрация электронов в металле.

· Удельная проводимость собственных полупроводников:

s = en(b_n + b_p),

где е – элементарный заряд; n – концентрация носителей тока электронов и дырок; b_n и b_p – подвижности электронов и дырок.

· Напряжение на гранях прямоугольного образца при эффекте Холла, холловская разность потенциалов:

U_H = R_HBja,

где R_H – постоянная Холла; В – магнитная индукция; j – плотность тока: а – ширина пластины (образца).

· Постоянная Холла для полупроводников типа алмаз, германий, кремний и других, обладающих носителями тока одного вида (n или p):

где n – концентрация носителей тока.

· Связь магнитной индукции 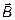с напряженностью магнитного поля в изотропном магнетике:

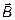= mm₀ ,

где m - магнитная проницаемость среды; m₀ = 4p^.10^-7 Гн/м – магнитная постоянная.

· Намагниченность однородного изотропного магнетика:

а) рассчитанная на единицу объема

;

б) молярная

в) удельная

.

где - магнитный момент i -той молекулы (атома); N – число молекул в объеме V; m - масса магнетика; M – молярная масса; r - плотностьмагнетика.

· Магнитная восприимчивость однородного изотропного магнетика:

а) рассчитанная на единицу объема

б) молярная

в) удельная

где Н – напряженность магнитного поля.

· Связь магнитной восприимчивости с магнитной проницаемостью:

m = 1 +c.

· Намагниченность при насыщении в случае однородного изотронного магнетика

,

где n – концентрация молекул атомов с магнитным моментом .

· Магнитная восприимчивость парамагнитного однородного изотропного магнетика при условии p_mВ<kT:

,

где k – постоянная Больцмана; Т – термодинамическая температура.

· Магнетон Бора:

где m – масса электрона; m_В = 0,927^.10^-23 Дж/Тл.

· Частота ларморовой прецессии:

где В – магнитная индукция.

Поиск по сайту: