АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 50

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. В некоторых странах, например в США, президента заменяет вице-
  3. Вания. Одной из таких областей является, например, регулирова-
  4. Виды знания. Контрпример стандартному пониманию знания
  5. Власть примера. Влияние с помощью харизмы
  6. Внешний долг (внешняя задолженность): пример России
  7. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  8. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  9. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  10. Второй пример абстрактного синтеза
  11. Выбор канала распределения. Факторы, влияющие на выбор канала распределения.. Пример выбора канала распределения.
  12. Выравнивание производства в системы управления производством на примере фирмы «Тойота».

Определить параметр а решетки и плотность р кристалла кальция, если расстояние d между ближайшими соседними атомами равно 0,393 нм. Решетка кубическая гранецентрированная.

 

 
 


Дано: Решение

 
 


d = 0,393 нм

а, р -? d

a

Рис.28

Параметр а решетки и расстояние d между ближайшими соседними атомами связаны простым геометрическим соотношением, ясным из рис.28:

а = d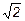

Подставляя в это выражение численное значение расстояния, получим

а = 0,393 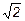нм = 0,556 нм = 5,56.10—10 м

Плотность r кристалла связана с молярной массой m и молярным объемом V0 соотношением

r = m /V0. (1)

Молярный объем V0 найдем как произведение объема а3 одной элементарной ячейки на число z0 элементарных ячеек, содержащихся в одном моле кристалла:

 

V0 = a3z0.

Учитывая, что число элементарных ячеек для кристалла, состоящего из одинаковых атомов, можно найти, разделив число Авогадро NA на число n атомов, приходившихся на одну элементарную ячейку, последнее равенство можно написать в виде

(2)

Подставив в (1) выражение V0 из (2), получим

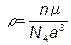
Подставив данные и учитывая, что число в случае кубической гранецентрированной решетки n = 4:

Проверка размерности: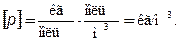

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)