Пример 34

Определить импульс р и кинетическую энергию Т электрона, движущегося со скоростью u = 0,9 с, где с – скорость света в вакууме.

Дано: Решение

u = 0,9 с Импульсом частицы называется произведение

р, Т -? ч астицы на ее скорость:

р = mu. (1)

Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле

(2)

где m – масса движущейся частицы; m₀ – масса покоящейся частицы; b = u/c – скорость частицы, выраженная в долях скорости света.

Заменив в формуле (1) массу m ее выражением (2), и приняв во внимание, что u = сb, получим выражение для релятивистского импульса

(3)

Подставим числовые значения величин, входящих в формулу (3):

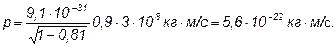
В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией Е и энергией покоя Е₀ этой частицы, т.е. Т = Е – Е₀. Так как Е = mc² и Е₀ = m₀c², то, учитывая зависимость массы от скорости, получим:

или

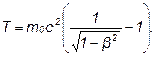
Подставив числовые данные, выраженные в единицах СИ, найдем . Во внесистемных единицах энергия покоя электрона m₀c =0,51МэВ. Подставив это значение в формулу (4), получим

Т = 0,52^.1,29 МэВ = 1,06^.10^-13 Дж.

Поиск по сайту: