Пример 2. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Dt = 2 с по линейному закону от I0=0 до I = 6 А (рис.3)

Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Dt = 2 с по линейному закону от I₀=0 до I = 6 А (рис.3). Определить теплоту Q₁, выделившуюся в этом проводнике за первую секунду, и Q₂ – за вторую, а также найти отношение Q₂/Q₁.

Дано:   Dt = 2 с I0 = 0 A I = 6 А Q1, Q2, Q2/Q1-?

Решение   I, A 6   3 0 1 2 t,c   Рис.3

Закон Джоуля-Ленца в виде Q = I²Rt справедлив для случая постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде:

dQ = I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В нашем случае

I = k t, (2)

где k – коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т.е.

С учетом (2) формула (1) примет вид

. (3)

Для определения теплоты, выделившейся за конечный промежуток времени Dt, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

При определении теплоты, выделившейся за первую секунду, пределы интегрирования t₁=0, t₂=I c и, следовательно,

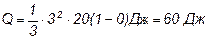
При определении теплоты Q₂ пределы интегрирования t₁ = I c, t₂ = 2 c, тогда

Дж.

Следовательно, Q₂/Q₁ = 420/60=7, т.е. за вторую секунду теплоты выделится в 7 раз больше, чем за первую.

Проверка размерности:

[ Q ] = .

Поиск по сайту: