Пример 33

Определить мощность, необходимую для того, чтобы поддерживать температуру расплавленной платины 1773⁰ С неизменной, если площадь ее поверхности 1,0 см². Считать платину абсолютно черным телом и потери энергии не учитывать. Чему равна длина волны в спектре излучения платины, на которую приходится максимальная энергия?

Дано: Решение

Т = 1773⁰ С Искомую мощность Р можно определить

S =10^{-4 м2} из соотношения Е = Рt, где Е – энергия,

s = 5,67^.10^-8 Вт/(м^2.К⁴) уносимая излучением с поверхности

b = 0,0029 м^.К пластины за время t, т.е. Е= ISt. Суммар-

Р,l¢ =? ная интенсивность излучения пластины

определяется законом Стефана-Больцмана

I = sT⁴ (1)

Поскольку Р = Е/t, имеем Р = IS/t = IS.

Заменяем I его значением, найденным из закона Стефана-Больцмана, получим

Р = sТ⁴S = 5,67^.10^-8 Вт/(м^2.К⁴)^.10^{-4 м2} = 99,4 Вт.

Проверка размерности: .

Длину волны l₀, на которую в спектре приходится максимум энергии, можно найти из закона Вина: l₀Т = b.

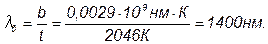
Проверка размерности: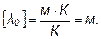

Поиск по сайту: