Пример 11

Электрон, пройдя ускоряющую разность потенциалов U=400 В, попал в однородное магнитное поле напряженностью Н=10³А/м. Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.

Дано Решение

U = 400 В Радиус кривизны траектории электрона определим

H = 10³ A/м исходя из следующих соображений: на движущийся

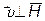в магнитном поле электрон действует сила Лоренца

R, n =? (действием силы тяжести можно пренебречь).

Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона можно записать F_л = ma_n, где a_n – нормальное ускорение или

(1)

где е – заряд электрона, u скорость электрона, В – магнитная индукция, m - масса электрона, R – радиус кривизны траектории, a - угол между направлением вектора скорости и вектором 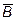(в данном случае ^ 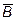и a = 90 ⁰, sin a = 1).

Из формулы (1) найдем

R = m / . (2)

Входящий в равенство (2) импульс может быть выражен через кинетическую энергию Т электрона:

. (3)

Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством

.

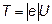Подставив это выражение Т в формулу (3), получим:

.

Магнитная индукция В может быть выражена через напряженность Н магнитного поля в вакууме:

В = m₀Н.

где m₀ – магнитная постоянная.

Подставив найденные выражения В и mu в формулу (2), определим

. (4)

Выразим все величины, входящие в формулу (4), в единицах СИ: m = 9,11^.10^{-31 кг; 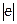- 1,60.}10^-19 Кл; U= 400 В; m₀ = 4p^.10^-7 Гн/м; H = 10³ А/м. Подставим эти значения в формулу (4) и произведем вычисления:

Для определения частоты обращения воспользуемся формулой, связывающей частоту со скоростью и радиусом:

n = u /pR× 2. (5)

Подставив в формулу (5) выражение (2) для радиуса кривизны, получим

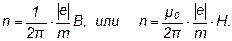
Все величины, входящие в эту формулу, ранее были выражены в единицах СИ. Подставим их и произведем вычисления:

Проверка размерности:

Поиск по сайту: