Пример 44

Энергия возбуждения атома водорода Е_в = 12,09 эВ. Определить возможные значения орбитального момента импульса L_i электрона в возбужденном состоянии этого атома.

Дано: Решение

Е_в = 12,09 эВ Орбитальный момент импульса L _i электрона оп-

n = l ределяется азимутальным квантовым числом l, кото-

L_l =? рое принимает значения от нуля до n – 1, где n – глав-

ное квантовое число:

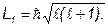
Так как ряд возможных значений l ограничен величиной n, то определим главное квантовое число. Собственные значения энергии электрона в атоме водороде определяются по формуле

Состояние электрона в атоме водорода с n = 1 является основным. В этом состоянии электрон обладает минимальной из дискретного ряда возможных для электронов энергией (Е₁ =-13,6 эВ). При возбуждении атома электрон переходит на n – уровень, характеризуемый энергией Е_n. Следовательно, разность между значениями энергий E₁ и E_n будет численно равна энергии возбуждения, т.е.

E₁ – E_n = E_в

Подставив числовые значения величин, выраженные в электрон-вольтах, получим 12,09 = - 13,6/n² + 13,6, откуда n = 3. Следовательно, l = 0,1,2, а орбитальные моменты импульса соответственно равны 0,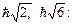

а) l = 0; L = 0;

б) l = 1: L =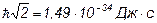

в) l = 2; L =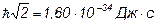

Поиск по сайту: