Инвестиционные операции и изменение стоимости денег во времени

Одним из важнейших свойств денежных потоков является их распределенность во времени. При анализе относительно краткосрочных периодов (до 1 года) в условиях стабильной экономики данное свойство оказывает относительно незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми остальными денежными потоками, что позволяет оперировать их итоговыми значениями. Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная проблема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, полученная предприятием с интервалом в 1 и более год, в таких условиях будет иметь для него неодинаковую ценность. Но проблема не сводится только к учету инфляции. Одним из основополагающих принципов финансового менеджмента является признание временной ценности денег, то есть зависимости их реальной стоимости от величины промежутка времени, остающегося до их получения или расходования.

Предоставляя кредит, владельцы денег устанавливают такие условия его возврата, которые по их мнению полностью возместят им все моральные и материальные неудобства, возникающие у человека, расстающегося (пусть даже и временно) с денежными знаками.

Количественной мерой величины этого возмещения является процентная ставка. С ее помощью может быть определена как будущая стоимость "сегодняшних" денег (например, если их собираются ссудить), так и настоящая (современная, текущая или приведенная) стоимость "завтрашних" денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг. В первом случае говорят об операции наращения, поэтому будущую стоимость денег часто называют наращенной (FV). Во втором случае выполняется дисконтирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость (PV). Для финансового менеджмента значительно более важное значение имеет дисконтировани е денежных потоков, приведение их будущей стоимости к современному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей. Сначала следует усвоить наиболее элементарные операции с единичными суммами (разовыми платежами).

Процентная ставка показывает степень интенсивности изменения стоимости денег во времени. Процентная ставка (r) является относительной величиной, измеряется в десятичных дробях или %, и определяется делением процентов на первоначальную сумму

(13.1)

Наращение первоначальной суммы по процентной ставке называется декурсивным методом начисления процентов.

Кроме процентной существует учетная ставка d (другое название – ставка дисконта), величина которой определяется по формуле:

(13.2)

Основной областью применения учетной ставки является дисконтирование, процесс, обратный по отношению к начислению процентов. Тем не менее, иногда она используется и для наращения. В этом случае говорят об антисипативных процентах.

При помощи рассмотренных выше ставок могут начисляться как простые так и сложные проценты. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов – в геометрической. Вначале более подробно рассмотрим операции с простыми процентами.

Сумму простых процентов (S) определяют по формуле

, где

(13.3)

T – продолжительность инвестиционной операции, измеренная в годах,

r – годовая ставка процентов.

В конце срока сделки сумма с процентами составит

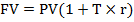. (13.4)

Для начисления сложных процентов используется формула

. (13.5)

Наращенная сумма с процентами в конце срока операции, которая продолжалась T лет, с ежегодным начислением сложных процентов по ставке r составит

FV = PV(1 + r)^Т. (13.6)

Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они называются годовыми. Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. То есть нет никакой разницы начислять 30% годовых 1 раз в год или начислить 2 раза по 15% годовых. Простая ставка 30% годовых при одном начислении в году называется эквивалентной простой ставке 15% годовых при начислении 1 раз в полгода.

Обычно в краткосрочных операциях (до одного года) доход на­числяется по формуле простых процентов, а при вложениях капита­ла на срок более одного года можно использовать формулу сложных процентов. Иногда (например, при высоком темпе инфляции), что­бы заинтересовать инвесторов, заемщик может предложить выплату дохода по схеме начисления сложных процентов несколько раз в год. В этом случае наращенную сумму определяют по формуле

, где

(13.7)

r – годовая ставка сложных процентов,

m – количество начис­лений процентов за год.

Можно использовать также формулу пересчета несколько раз в год по годовой ставке учетного процента d

.

(13.8)

Если продолжительность сделки превышает один год, но насчиты­вает нецелое количество лет, можно применять комбинированную схему начисления дохода: сложные проценты – за целое количество лет, простые – за неполную часть года. При этом наращенную сум­му определяют по формуле

,

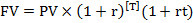(13.9)

где [T] – целое количество лет,

t = T – [T] – дробная часть числа (неполная часть года).

Зная годовую процентную или учетную ставку, можно определить наращенную стоимость при краткосрочных финансовых вложениях (на срок менее одного года). Для этого надо установить продолжи­тельность финансовой операции и условия расчетов – обыкновен­ный или точный процент; при этом день выдачи и погашения креди­та считается как один день. В различных случаях могут применяться различные способы подсчета числа дней в году (соглашение по подсчету дней). Год может приниматься равным 365 или 360 дням (12 полных месяцев по 30 дней в каждом).

Если временная база принимается равной 365 (366) дням, то проценты называются точными. Если временная база равна 360 дням, то говорят о коммерческих или обыкновенных процентах.

Размер обыкновенного процента рассчитывается по формуле

, где (13.10)

t – продолжительность операции, дней,

r – годовая процентная ставка.

Наращенная сумма при этом определяется по формуле

, (13.11)

При использовании годовой учетной ставки d получаем

. (13.12)

Наращенная сумма будет равна

. (13.13)

Формула расчета точного процента имеет следующий вид

. (13.14)

Наращенная сумма при этом равна

. (13.15)

При использовании годовой учетной ставки d, получаем

. (13.16)

Наращенная сумма при этом будет равна

. (13.17)

Обратной задачей по отношению к начислению процентов является расчет современной стоимости будущих денежных поступлений (платежей) или дисконтирование. В зависимости от того, какая именно ставка – простая процентная или простая учетная – применяется для дисконтирования, различают два его вида:

- математическое дисконтирование;

- банковский учет.

Рассмотрим формулы математического дисконтирования:

1. При начислении дохода по формуле простых процентов

. (13.18)

. (13.19)

. (13.20)

2. При начислении дохода по формуле сложных процентов

, (13.21)

, (13.22)

Математическое дисконтирование используют в методиках оцен­ки эффективности инвестиционных проектов, учитывающих влияние фактора времени на будущие денежные потоки. Эти методики пре­дусматривают расчет определенных показателей. Рассмотрим их.

Денежный поток – это разность между всеми денежными посту­плениями за определенный период и денежными затратами предпри­ятия за этот же период, т. е. сумма чистой прибыли и амортизации.

Дисконтная ставка – это процентная ставка (r),используемая для расчетов приведенной (нынешней) стоимости будущих денежных по­токов.

Коэффициенты дисконтирования – это понижающие коэффициен­ты, используемые в расчете приведенной (нынешней) стоимости будущих доходов: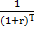

Дисконтированный денежный поток – это стоимость на сегодняш­ний день будущих доходов с учетом потери части стоимости денег со временем:

Чистая нынешняя (приведенная) стоимость проекта (NPV – Net Present Valye) – это разность между дисконтированной (нынешней) стоимостью будущих денежных потоков и первоначальными инвестициями по проекту.

Если NPV положительна, проект является экономически приемле­мым, если отрицательна, то проект невыгоден для инвесторов, так как в этом случае будущие доходы (с учетом их обесценивания во вре­мени) не возмещают первоначальных инвестиций.

В банковских расчетах, связанных с покупкой (учетом) векселей или других краткосрочных обязательств, применяются формулы банковского (коммерческого учета). Рассмотрим основные из них:

,

(13.23)

,

(13.24)

.

(13.25)

Основные правила процентных вычислений, рассмотренные ранее, остаются неизменными и для совокупности платежей, однако возникает необходимость ввести несколько дополнительных понятий. Для обозначения денежных потоков в наиболее общем смысле используется термин рента. Каждый отдельный рентный платеж называют членом ренты. Частным случаем ренты является финансовая рента или аннуитет – такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними. Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет.

По величине членов денежного потока ренты могут быть:

- постоянными (с равными членами);

- переменными.

По вероятности выплат ренты делятся на:

- верные;

- условные.

По своей общей продолжительности (или по числу членов) различают:

- ограниченные (с конечным числом членов);

- бесконечные (вечные, бессрочные) ренты.

По отношению к фиксированному моменту начала выплат ренты могут быть:

- немедленными;

- отложенными (отсроченными).

Ренты, платежи по которым производятся в конце периода называются обычными или постнумерандо; при выплатах в начале периода говорят о рентах пренумерандо.

Если член ренты R неизменен в течение всего срока, процентная ставка r также постоянна, то определяют наращенную (будущую) стоимость аннуитета от ежегодных платежей одинакового размера (А) по формуле

, где

(13.26)

К_r,n - аккумулирующий коэффициент наращения при заданной годичной процентной ставке r и количестве лет n, который определяется по формуле

.

(13.27)

Приведенная (нынешняя) стоимость аннуитета определяется путем приведения ежегодных платежей к исходному моменту (первому платежу) с учетом дисконтирования платежей, осуществляемых в будущем по формуле

, где

(13.28)

– аккумулирующий коэффициент дисконтирования при заданной годичной процентной ставке r и количестве лет n, определяется по формуле

.

(13.29)

Существуют финансовые инструменты, предполагающие бессрочную выплату доходов их держателям. Для определения приведенной стоимости вечного аннуитета применяют формулу

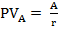, где

(13.30)

PV_A – член ренты (вечный аннуитет).

Таким образом, чтобы получить доход при инвестировании капитала необходимо учитывать, что деньги со временем обесцениваются. Для того, чтобы учесть изменение стоимости денег во времени проводятся расчеты наращивания стоимости капитала при различных схемах начисления простых и сложных процентов, современной (нынешней) стоимости капитала путем математического и банковского дисконтирования, наращенной и приведенной стоимости денежных потоков и т.д.

Поиск по сайту: