Регрессионного анализа в моделировании массовой оценки недвижимости

Эффективное применение оценщиком «оценочных» моделей во многом предопределяется не только его глубокими профессиональными знаниями рынка недвижимости, но и владением аппарата МРА (линейного и нелинейного). Речь идет о возможности оценщика дать квалифицированное заключение по результатам модельных расчетов стоимости недвижимости. А по существу дать определенный ответ: насколько модельная рассчетная стоимость недвижимости адекватна объективно сложившейся на рынке стоимости? С помощью категорий математической статистики можно дать ответ на этот вопрос, проанализировав соответствующие статистические характеристики используемой «оценочной» модели относительно ее адекватности объективной реальности. Например, можно использовать семь статистических характеристик, первые три из которых рассмариваются как мера согласия сформулированной модели, отражают запредиктивную точность (истинность) используемых математических зависимостей (уравнений). К ним относят коэффициент определенности (детерминации) (D²), среднеквадратическую ошибку (а) и коэффициент вариации (С). Каждая из этих характеристик отражает степень адекватности используемых в модели статистических уравнений. Вторая группа статистических характеристик определяет статистическую значимость отдельных переменных моделей: коэффициент корреляции (r), критерии Стьюдента и Фишера и бета-коэффициент.

Коэффициент определенности (детерминации) (D²). По определению из любой регрессионной модели можно определить параметры (bp, b,..., Ь) при соответствующих независимых переменных и остаточную дисперсию (отклонения). Последняя отражает вариацию

переменных от их средних значений («остатки») «не объяснимых» данной регрессионной моделью. Тогда коэффициент определенности детерминации в контексте рассматриваемых «оценочных» моделей можно рассчитать по формуле

i< ъ-ъ²

l(pi-p)²

I-l

где и Pi - цена сделки с i-й недвижимостью и цена сделки с i-и недвижимостью «не объяснимой» регрессионной моделью соответственно; Р - средняя цена сделок с недвижимостью.

Таким образом, величина D² соответствует доле (проценту) цен, «объяс нимых» регрессионной моделью. Этот коэффициент может принимать значения в интервале от 0 до 1. Когда D = О, никакая вариация (отклонение от средней цены) цен «не объясняется» моделью. Наоборот, когда

D² = 1, все отклонения от средней цены Р «объясняются» уравнения\ регрессии.

Среднеквадратическая ошибка модели (а) измеряет величину отклоь ния расчетных (прогнозных) цен продаж, получаемых из регрессионной модели, от фактически сложившихся цен продаж на рынке. Она определяется по формуле _

Ы_____

где р. и P_t - расчетная (прогнозная) и фактическая цены продаж недвижимости соответственно; п - количество продаж;

к - число независимых переменных, рассматриваемых в регрессионной

модели.

Величина а представляет собой меру среднеквадратической ошибки или дисперсию регрессионной модели. Извлечение квадратного корня позволяет получить значение такой ошибки, которую можно рассматривать как среднеквадратическое отклонение ошибок регрессионной модели в отличие от коэффициента D², который выражается в долях (в процентах), а измеряет отклонения (погрешность) в стоимостном выражении. Существующее программное обеспечение регрессионного анализа позволяет вычислить не только значение а, но и соответствующие доверительные интервалы для расчетной (модельной) стоимости по отдельным объектам недвижимости. Эта стоимость является функцией от а и индивидуальных (количественных и качественных) параметров конкретных объектов недвижимости. Чем ближе параметры объекта недвижимости к параметрам типового объекта (их значения ближе к средним значениям), тем меньше среднеквадратическая ошибка и доверительный интервал расчетной (модельной) стоимости.

Коэффициент вариации (C_v) в регрессионном анализе определяется как отношение а к средней цене продажи (сделки):

Коэффициент C_v аналогичен показателю коэффициента вариации, ис­пользуемого при анализе вариационного ряда и определяемого как отно­шение среднеквадратического отклонения цен продаж к средней цене. Если предположить, что рассчитанная среднеквадратическая ошибка по рас­сматриваемой регрессионной модели составила, например, 5000 у.е., а средняя цена сделок с недвижимостью определена на уровне 50 000 у.е., то коэффициент вариации будет равен (5000/50 000 • 100% = 10%). Это означает, что при нормальном распределении случайных величин (цен продаж на рынке недвижимости) примерно ²/₃ расчетных (модельных) цен из регрессионной модели находятся в пределах 10%-ных отклонений от средних цен. Такой результат моделирования стоимости недвижимости можно рассматривать как, безусловно, хороший.

Коэффициент корреляции (г) является одной из статистических характеристик, относящихся к анализу значимости отдельных переменных регрессионной модели. Он служит мерой линейной зависимости между двумя переменными, принимая значения в интервале от -1 до +1. При этом необходимо иметь в виду, что нулевое или близкое к нулю значение г не означает «отсутствие» зависимости (между двумя переменными), а лишь Указывает на «отсутствие» линейной зависимости (может быть еще и нелинейная зависимость).

Как правило, существующее компьютерное программное обеспечение °зволяет рассчитать корреляционную матрицу коэффициентов корреля­ции между всеми парами переменных. При анализе корреляции той или Ной независимой переменной с зависимой переменной следует иметь в виду, что коэффициент корреляции является безразмерной величиной ил процентным отношением, отражающим наличие только линейной зави симости между двумя переменными. Например, рассчитаны два коэффициента корреляции, отражающие тесноту связи: между ценой и пл щадью объекта недвижимости r = 0,92 и ценой и местоположением r= 0,62. Это позволяет лишь утверждать, что для рассматриваемых двух пар существует линейная зависимость и для первой пары (стоимость объекта недвижимости от его площади) эта зависимость более существенна дл данного регионального рынка недвижимости.

Критерий Стьюдента (t - статистика) показывает меру значимости (или весомости) переменной регрессии на изменения зависимой переменной (цены сделки) и вычисляется как отношение соответствующего коэффициента регрессии (Ь) к его среднеквадратической ошибке (s_b):

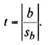
Величина s_b характеризует среднеквадратическое отклонение коэффициента регрессии Ь и отражает погрешность при использовании этого коэффициента в качестве статистической характеристики связи независимой переменной X. и зависимой переменной Р. В том случае, если значение t достаточно велико, то есть основание считать, что X. является значимой переменной при расчете Р (цены продажи). Наоборот, если значение t мало, то можно предположить нулевое значение соответствующего коэффициента регрессии Ь., а также и несущественную значимость независимой переменной X. для моделируемой цены продажи Р.

Для данного критерия имеется Специальная таблица, по которой мож­но определить его значение, исходя из числа степеней свободы (n-k-l), где п - число переменных; к - количество независимых переменных. В общем случае, при достаточно большой статистической выборке (не менее 50 объектов недвижимости) значение t-статистики более ±2,00 свидетельствует о существенной значимости соответствующей независимой переменной, так как при таком табличном значении t - распределения Стьюдента нулевая гипотеза о равенстве нулю коэффициента регрессии отвергается (считается значимым). Предположим, что для 60 сделок недвижимостью (число степеней свободы равно 58) t -статистика для не: висимой переменной - площадь объекта - определена на уровне 8,3. Табличное значение t -распределения Стьюдента для числа степеней своб 58 равно ± 2,001, при котором с вероятностью 95% можно утверждать что коэффициент регрессии не равен нулю. Следовательно, в данном слу чае при моделировании стоимости недвижимости площадь является с щественной независимой переменной.

Критерий Фишера (F-статистика) связан с критерием Стьюдента и также используется для определения значимости независимых переменных

регрессионной модели. В МРА математическая зависимость критериев Стьюдента и Фишера определяется уравнением

Для определения этого критерия также имеются таблицы как в спе­циальной литературе, так и в учебниках по математической статистике. g общем случае при достаточно большой выборке табличное значение f- статистики, превышающее 4,0, указывает на то, что соответствующая независимая переменная значима при моделировании Р (стоимости не­движимости) с вероятностью 95%.

Бета-коэффициенты представляют собой «нормированные» коэффи­циенты регрессии, являющиеся мерой значимости отдельных переменных относительно друг друга. Бета-коэффициенты и коэффициенты регрессии связаны между собой следующим уравнением

где s. - среднеквадратическое отклонение X.; s - среднеквадратическое отклонение Р.

Бета-коэффициенты эффективны, если необходимо сравнить относительную значимость независимых переменных. Допустим, например, что оценщику нужно определить: какая из двух переменных - площадь или эффективный возраст недвижимости - более значима для стоимости объекта недвижимости. Поскольку площадь измеряется в квадратных метрах, а эффективный возраст - в годах, коэффициенты регрессии нельзя сравнит непосредственно. Если обе переменные нормировать, то можно осуще ствить такое сравнение. Допустим, что бета-коэффициент для площад равен 0,3, а для эффективного возраста - (-0,45). Это означает, что пр постоянных значениях остальных независимых переменных регрессной ной модели увеличение площади, например на 10%, вызовет увеличена стоимости недвижимости на 3%. Аналогично, увеличение эффективног возраста на 10% снизит стоимость недвижимости на 4,5%. В данном ел} чае, эффективный возраст в большей степени влияет на изменение стог мости недвижимости, чем ее площадь.

Приведенные выше статистические характеристики в МРА можно рассматривать не только как оценочные параметры адекватности модели объективным реалиям, но и как инструмент калибровки модели посредством введения соответствующих корректировок. Существующее компьютерное программное обеспечение позволяет

квалифицированному оценщику проводить такого рода «настройку» модели, работая в диалоговом режиме с компьютером.

Пример. Рассмотрим применение некоторых указанных выше статистических характеристик в МРА. Предположим, что с помощью компьютерной программы проведен регрессионный анализ рыночных данных по сделкам с жилой недвижимостью.

Результаты этого анализа на п- м этапе моделирования распечатаны (или представлены на дисплее компьютера в следующем виде (табл. 15.6).

Критерий D² равен 0,9456, что означает 94,5% вариаций (отклонений) цен продаж квартир от средней цены «объясняются» регрессионной моде­лью; абсолютная вариация цен продаж от средней составляет 1183,150 у.е. (среднеквадратическая ошибка а), а коэффициент вариации С_у, равный 0,0680, свидетельствует о том, что две трети расчетных (модельных) цен из регрессионной модели находятся в пределах 6,8% вариаций (отклон< ний) от средних цен (при нормальном распределении случайных велич на рынке - цен продаж). Все это позволяет сделать вывод о высокой о гласованности модели объективно сложившейся на рынке жилья конъ* ктуры относительно рассматриваемых пяти факторов (независимых переменных).

Используя расчетные значения t -статистик (критерия Стьюдента), можно проранжировать независимые переменные по степени значимости их влияния на стоимость квартиры: 1) общая площадь; 2) возраст здания 3) количество комнат; 4) средняя этажность квартиры; 5) наличие балкона. Как видно, наиболее существенно влияет на стоимость квартиры её общая площадь (t = 13,27), а наименее существенно - наличие балкона (t = 1,64).

Уравнение (модель) стоимости квартиры (V) можно сформулировать в аналитической форме, используя полученные из регрессионной модели коэффициенты регрессии:

V- -16414,387 + 316,617 • X, + 10620,255 • Х₂ + + 6816,231 • Х₃ - 60,345 • Х4

+ 2025,236 • Ху

Имея соответствующие параметры той или иной квартиры, расположенной в рассматриваемом районе, можно рассчитать ее стоимость. Например, необходимо оценить стоимость квартиры для целей налогообложения, которая характеризуется следующими параметрами: общая площадь - 53,4 м² находится на среднем этаже (не первый и не последний этажи); имеет балкон; ее возраст - 15 лет; состоит из двух комнат. Качественные характеристики квартиры (средняя этажность и наличие балкона) в модели закодированы бинарными переменными. Подставив эти значения независимых переменных в уравнение стоимости квартиры, получим:

V = -16414,387 + 316,617 • 53,4 + 10620,255 • 1 + 6816,231 • 1 -- 60,345 • 15 +

2025,236 • 2 = 21074,743 у.е.

Таким образом, стоимость оцениваемой двухкомнатной квартиры со­ставит 21 000 у.е.

Тесты

1. Имеется статистическая выборка из 11 квартир, в которых кухни следующих размеров (м^[4]): 5; 9; 8,5; 6,2; 10; 8; 7; 9,5; 6,5; 9,6; 8,4. Каковы медианное и среднее значения, вариационный размах (диапазон) и среднеквадратическое (стандартное) отклонение?

2. Какой из нижеприведенных вариантов параметров объектов недвижимости необходимо отнести к «качественному» виду?

А. Тип внешних стен. Б. Тип ванной комнаты. В. Вид из окон. Г Все вышеперечисленное.

3. Какой из нижеприведенных вариантов параметров объекта недвижимости необходимо отнести к «количественному» виду?

А. Жилая площадь. Б. Размер кухни. В. Размер гаража; Г. Все выше перечисленное.

4. На рынке продано 6 квартир по следующим ценам (у.е.): 25 000; 28 125; 6250; 19 000; 3125; 4500. Необходимо ответить на следующие вопросы:

A. Могут ли все эти квартиры находиться в одном и том же микрорайоне со стандартной застройкой? Б. Какова средняя цена продажи (по медиане)?

B. Какова средняя цена продажи (по средней арифметической)? Г. Является ли средняя цена продажи разумной?

5. Какие из нижеперечисленных параметров жилого многоквартирного дома являются количественными и качественными и какие из этих параметров можно ввести в «оценочную» модель с помощью бинарных переменных?

1) цена предложения квартиры;

2) номер этажа, где расположена квартира;

3) количество этажей в жилом доме;

4) категория дома (типовая, нетиповая);

5) общая площадь квартиры;

6) площадь кухни;

7) совершенность сделки (продана или не продана квартира на дату оценки);

8) вид строительного материала жилого дома (кирпич или иное),

9) вид из окон.

Приложение I Отчет об оценке

рыночной стоимости трехкомнатной 1 квартиры

Уважаемый

В соответствии с договором №..., заключенным между Вами и обще ством с ограниченной ответственностью, в лице генерального директора, произведена оценка ОБЪЕКТА, включающего в себя трехкомнатную квар тиру, расположенную по адресу:

по состоянию на 24 марта 2001 г.

Целью оценки является определение рыночной стоимости ОБЪЕКТА для реализации имущественных прав.

Обращаю внимание, что это письмо не является отчетом по оценке, а только предваряет отчет, приведенный далее. Полная характеристика ОБЪЕКТА оценки, необходимая информация и расчеты представлены в отчете, отдельные части которого не могут трактоваться раздельно, а только в связи с полным его текстом, с учетом всех принятых допущений и ограничений.

Произведенные ниже расчеты и анализ позволяют сделать вывод, что рыночная стоимость ОБЪЕКТА оценки, включающего в себя трехкомнат ную квартиру, расположенную по адресу:

по состоянию на 24 марта 2001 г., с учетом округления составляет

706 000 руб. (Семьсот шесть тысяч руб.)

Настоящий отчет составлен в соответствии с Федеральным законом «Об оценочной деятельности в Российской Федерации» от 29 июля 1998 г. •№ 135-ФЗ; с государственными стандартами: ГОСТ Р 51195.0.01-98 «Единая система оценки имущества. Основные положения», ГОСТ Р 51195.0.02- о «Единая система оценки имущества. Термины и определения» от 1 ян­варя 1999 г.; стандартами Российского общества оценщиков: СТО РОО 27-01-95 «Кодекс профессиональной этики членов РОО», СТО РОО 20-01- СТО РОО 20-02-96, СТО РОО 20-03-96, СТО РОО 20-05-96, СТО РОО 1-01-95, СТО РОО 22-01-96, «Едиными стандартами профессиональной

практики оценки» и «Международными стандартами оценки», Международного комитета по стандартам оценки имущества (TIAVSC).

Если у Вас возникнут какие-либо вопросы, пожалуйста, обращайте непосредственно к нам.

Благодарим Вас за возможность оказать Вам услуги! Генеральный директор

План отчета по оценке

Поиск по сайту: