Формы записи линеаризованных уравнений

В теории управления принято записывать дифференциальные уравнения в двух стандартных формах.

В общем виде линеаризованное дифференциальное уравнение, описывающее элемент, можно записать следующим образом

(2.7)

где y(t), x(t), f(t) - выходная и входная величины элемента и внешнее воздействие; a_i, b_i, c_i - постоянные коэффициенты; n - порядок уравнения, причем (n ≥ m,k); это условие физической реализуемости элемента, показывающее, что сигнал на выходе реального элемента не может возникнуть раньше подачи воздействия на его вход, т.е.

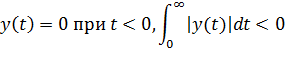
Уравнение (2.7) удобнее записывать в символическом виде, введя алгебраизированный символ дифференцирования p = d/dt. В результате уравнение примет вид

(2.8)

В общем случае в соответствии с (2.8) уравнение элемента можно представить в форме

При этом

полиномы степени n, m, k от символа дифференцирования p.

Первая стандартная форма записи. Дифференциальное уравнение записывают так, чтобы выходная величина и ее производные находились в левой части уравнения, а входные величины и все остальные члены - в правой. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести уравнение (2.8) к такому виду, разделим левую и правую его части на a_n и получим

(2.10)

При записи уравнения в первой стандартной форме (2.10) получившиеся

коэффициенты: Т_n, Т_n-1,…, Т₁ называются постоянными времени, они имеют размерность времени [с] и характеризуют инерционные свойства элемента; а k₁, …, k_m+1, k_m+2,…, k_m+k+2, называются коэффициентами передачи. Они представляют собой весовые коэффициенты, показывающие какой вклад в формирование выходной величины элемента вносит каждое слагаемое правой части уравнения.

Вторая стандартная форма записи. Для решения дифференциальных уравнений широкое распространение получил операторный метод, при использовании которого задача нахождения решения дифференциального уравнения сводится к алгебраическим действиям. Чтобы перейти от исходного дифференциального уравнения элемента при нулевых начальных условиях к операторному, необходимо в дифференциальном уравнении вместо реальных функций времени записать их изображения по Лапласу, а в полиномах символ дифференцирования p заменить на оператор Лапласа s.

Применив к дифференциальному уравнению (2.9) преобразование Лапласа, получим

uде s – оператор Лапласа; Y(s), X(s), F(s) - изображения по Лапласу выходной и входной величин элемента и внешнего воздействия;

полиномы степени n, m, k от оператора Лапласа s.

Оператор Лапласа s представляет собой комплексную величину, причем

s=c+jω,

где: c=Re s - абсцисса абсолютной сходимости; ω=Im s –угловая частота, имеющая размерность [рад/с].

Для перехода от реальных функций времени - оригиналов к их изображениям по Лапласу и наоборот введены прямое и обратное интегральные преобразования вида:

На практике для этих целей используют специальные таблицы [1,7].

Уравнения (2.9) и (2.11) формально совпадают между собой. Однако уравнение (2.9) является дифференциальным, куда входят реальные функции времени, а уравнение (2.11) - алгебраическим относительно изображений функций времени по Лапласу.

После ввода следующих обозначений:

уравнение (2.11) примет вид, являющийся второй стандартной формой записи

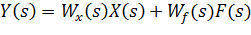
(2.12)

Выражения W_x(s) и W_f(s) в теории управления называются передаточными функциями.

Если f(t) = 0, то F(s) = 0 и тогда = - передаточная функция элемента по входу Х.

Eсли x(t)=0, то X(s)=0 и тогда 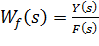= - передаточная функция элемента по входу F.

Поиск по сайту: