 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частотные характеристики. Частотные характеристики дают представление о передаточных свойствах САУ или элемента при изменении частоты входного сигнала
Частотные характеристики дают представление о передаточных свойствах САУ или элемента при изменении частоты входного сигнала.
Пусть на входе элемента действует гармонические колебания с постоянной амплитудой и частотой:
После перехода элемента в равновесный (статический) режим на его выходе устанавливается также гармонические колебания с той же частотой, но возможно, с другой амплитудой и, возможно, сдвинутые по фазе относительно x(t):
Если представить, что на вход элемента последовательно подаются указанные колебания, частота которых увеличивается с некоторым шагом, и фиксируется соответствующие Авых и 
, то при достаточно большом количестве таких экспериментов будет известно, как передаются на выход элемента колебания заданного частотного диапазона (как элемент воздействует на Авых и при разных частотах).
Если записать модели колебаний на входе и выходе в комплексной форме:
, то
взяв отношение:
Получим некоторую функцию 
, которая позволит выяснить, как изменяется амплитуда и фаза выходного сигнала при изменении частоты входного в бесконечном диапазоне частот.
Функция называется комплексно-частотной и может быть получена непосредственно из W(p) путем подстановки 
(подробнее см. свойства преобразования Лапласа). < пояснить про изображение комплексных чисел >
График называется АФЧХ: геометрическое место концов векторов комплексно-частотной функции при изменении частоты от нуля до бесконечности.
АФЧХ – основная частотная характеристика. Однако на практике ей пользоваться неудобно, не смотря на то, что она связывает сразу все параметры.
Удобнее анализировать две взаимосвязанные функции модуля и аргумента 
, объединенные общим параметром ω. При этом обе функции вещественные и позволяют определить положение вектора АФЧХ для заданной частоты. (рис.3.7)
Рис.3.7. Положение вектора АФЧХ для заданной частоты
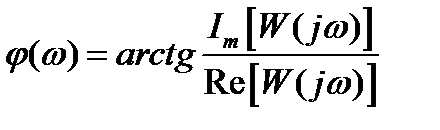– АЧХ
– ФЧХ
Иногда нужны:
– вещественная ЧХ
– мнимая ЧХ
Поиск по сайту: