Оценка работы линейных автоматических систем при случайных стационарных воздействиях

Оценить работу автоматических систем при сигналах внешних воздействий в виде стационарных случайных процессов можно с помощью корреляционных функций и спектральных плотностей.

Если задающее воздействие g(t) является случайным процессом, то выходная координата системы y(t) и ошибка воспроизведения x(t)=g(t)−y(t) представляют собой также случайные процессы.

Следовательно, при случайных воздействиях речь может идти об определении не мгновенных, а лишь некоторых средних значений выходной переменной системы и ошибки.

Такими средними значениями являются среднее значение квадрата выходной переменной системы

,

(14.20)

и квадрата ошибки

,

(14.21)

Эти величины можно найти через их корреляционные функции и спектральные плотности

,	(14.22)
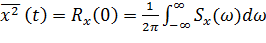,	(14.23)

Следовательно, для исследования статистической точности автоматических систем необходимо вычисление корреляционных функций R_y(τ), R_x(τ) и спектральных плотностей S_y(ω), S_x(ω) переменной на выходе системы y и ошибки x по известной корреляционной функции R_g(τ) и спектральной плотности S_g(ω) случайного входного воздействия.

Для установления взаимосвязи между корреляционными функциями переменных входа и выхода системы, а также взаимосвязи между их спектральными плотностями используется известное интегральное уравнение (интеграл Дюамеля), на основании которого

,

(14.24)

где w_y(t) - весовая или импульсная функция замкнутой системы по задающему воздействию g(t); λ - вспомогательное время интегрирования.

Тогда корреляционная функция выходной величины

,

(14.25)

а спектральная плотность, определяемая как прямое преобразование Фурье от корреляционной функции, имеет вид

.

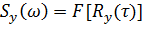(14.26)

Выполнив необходимые преобразования получаем

.

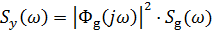(14.27)

где Фg(jω) - частотная передаточная функция замкнутой системы по задающему воздействию.

Таким образом, спектральная плотность выходной координаты системы может быть получена умножением спектральной плотности входной величины на квадрат модуля частотной передаточной функции замкнутой системы по задающему воздействию.

Аналогично получается выражение для спектральной плотности ошибки

,

(14.28)

где Ф_xg(jω) - частотная передаточная функция замкнутой системы по ошибке относительно задающего воздействия.

Выражения (14.27) и (14.28) устанавливают связь между спектральными плотностями S_y(ω), S_x(ω) переменной на выходе системы y и ошибки x со спектральной плотности S_g(ω) случайного входного воздействия.

Тогда средние значения квадрата выходной величины системы и ошибки определяются как

,	(14.29)
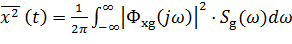,	(14.30)

При действии на систему независимых друг от друга задающего и возмущающего воздействий g(t) и f(t) спектральная плотность ошибки системы будет

,

(14.31)

где Ф_xf(jω) - частотная передаточная функция замкнутой системы относительно точек входа помехи f(t) и ошибки x(t); S_f(ω) - спектральная плотность сигнала помехи f(t).

Суммарная ошибка системы в этом случае будет характеризоваться выражением

,

(14.32)

Таким образом оценивается работа линейных автоматических систем при случайных стационарных воздействиях.

Контрольные вопросы

1. Дайте определение статистической динамики систем управления.

2. Изобразите базовую структуру модели системы при случайных воздействиях.

3. Перечислите и определите статистические характеристики случайных процессов.

4. Каково свойство эргодической гипотезы?

5. Поясните физический смысл корреляционной функции и спектральной плотности случайного процесса.

6. Каким образом производится оценка работы линейных систем при случайных стационарных сигналах?

7. Как определяется спектральная плотность выходной величины и ошибки системы?

8. Дайте определение средней квадратической ошибки системы и укажите способы ее вычислений.

9. Поясните постановку задачи синтеза оптимальных систем.

10. Каким образом вычисляются значения оптимальных параметров систем из условия минимума средней квадратической ошибки?

Поиск по сайту: