 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Последовательная коррекция динамических свойств. Последовательные корректирующие звенья можно разделить на три типа: пропорционально-дифференцирующие (ПД)
Последовательные корректирующие звенья можно разделить на три типа: пропорционально-дифференцирующие (ПД), пропорционально-интегри-рующие (ПИ) и пропорционально-интегро-дифференцирующие (ПИД) звенья.
ПД-звено имеет передаточную функцию
WПД(p)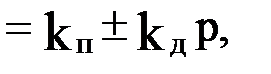 
то есть выходная величина этого звена пропорциональна входной величине и ее первой производной.
Включение этого звена в САУ приводит к тому, что передаточная функция разомкнутого контура САУ
умножается на WПД(p), то есть принимает вид
W(p) WПД(p) 
В результате характеристический полином замкнутой САУ D(р) будет следующий:
где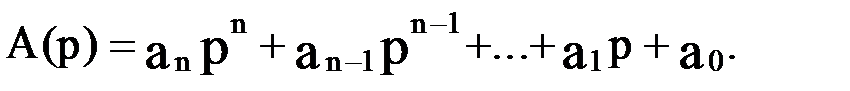 
Положим, что В(р)=k (так как мы исследуем влияние ПД-звена, то логично предположить, что в исходной САУ такого звена не было, но тогда числитель передаточной функции исходной САУ содержит лишь величину k). Тогда можно видеть, что в характеристическом полиноме замкнутой САУ изменится коэффициент при р в первой степени. Включение двух ПД-звеньев приведет к изменению коэффициента и при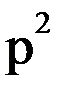 
и т.д. Изменение же этих коэффициентов изменяет условия устойчивости и качество переходного процесса.
Рассмотрим в качестве примера применение данного звена для стабилизации, то есть обеспечения устойчивости САУ с астатизмом выше первого порядка (порядок астатизма - это число интегрирующих звеньев в приведенной одноконтурной САУ).
Передаточную функцию разомкнутой САУ с порядком астатизма, равным r, можно представить в виде:
Соответственно характеристический полином замкнутой САУ будет:
D(р)=В(р)+ 
.
Если В(р)=k, то из последнего выражения следует вывод о том, что САУ с порядком астатизма r>1 являются структурно неустойчивыми, поскольку в D(р) отсутствуют члены с р в степени от единицы до (r-1) (по критерию устойчивости Гурвица).
Введем теперь в систему (r-1) ПД-звеньев. При этом в характеристическом полиноме появятся недостающие звенья:
Следовательно, САУ становится структурно устойчивой.
Влияние ПД-звена на качество переходного процесса продемонстрируем на примере последовательного соединения этого звена с апериодическим звеном с передаточной функцией
Передаточная функция последовательного соединения этих звеньев:
W0(p)WПД(р) 
Соответственно переходная функция
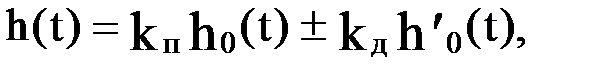
где 
- переходная функция апериодического звена.
Из последнего выражения видно, что отрицательное дополнительное воздействие по производной снижает быстродействие, а положительное, наоборот, повышает его. Например, при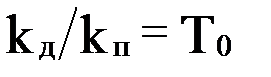 
полностью компенсируется инерционность апериодического звена:
W0(p)WПД(р) 
Реальные ПД-звенья обладают инерционностью, то есть имеют следующую передаточную функцию:
WПД(р) 
где ТПД 
Все сказанное выше об идеальном ПД-звене справедливо и для реального с той только разницей, что реальное слабее влияет на быстродействие и на области устойчивости.
ЛАЧХ реального ПД-звена приведена на рис.11.10.
Рис.11.10
ПД-звено является фильтром верхних частот, так как его ЛАЧХ растет с увеличением частоты. Поэтому введение этого звена в САУ расширяет ее полосу пропускания, повышает быстродействие.
Практически наиболее просто ПД-звенья реализуются в электрических системах постоянного тока, где они представляют собой пассивные RC- и RL- цепочки.
Пример реализации ПД-звена на операционном усилителе приведен на рис.11.11.
Рис.11.11
Пропорционально-интегрирующее (ПИ) звено имеет передаточную функцию
WПИ(р)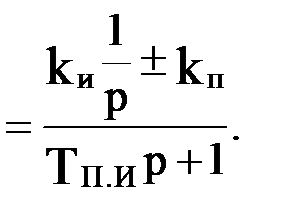 
В случае ТПИ=0 получаем идеальное ПИ-звено.
Последнее выражение можно представить так:
WПИ(р) 
Таким образом, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена. По своим частотным свойствам ПИ-звено противоположно ПД-звену, являясь фильтром нижних частот. ЛАЧХ ПИ-звена приведена на рис.11.12.
Рис. 11.12
Передаточная функция пропорционально-интегро-дифференциру-ющего (ПИД) звена
Это звено эквивалентно последовательному соединению интегрирующего звена и пропорционально-дифференцирующего с воздействием по двум производным или, что то же самое, последовательному соединению ПИ-звена и ПД-звена с одной производной. Таким образом, ПИД-звено повышает порядок астатизма, как и ПИ-звено, но при этом одновременно дает более сильную коррекцию динамических свойств САУ.
Такое звено подчеркивает как нижние, так и средние частоты, подавляя средние, как видно из приближенной ЛАЧХ ПИД-звена, приведенной на рис.11.13.
Рис.11.13
В связи с видом ЛАЧХ ПИД-звеньями называют не только звенья с указанной выше передаточной функцией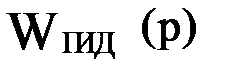 
, но и любые другие звенья, ЛАЧХ которых имеет минимум на средних частотах и растет в сторону как низких, так и высоких частот.
Вообще указанные выше наименования типов последовательных корректирующих звеньев в значительной степени условны, прежде всего, из-за инерционности реальных корректирующих звеньев.
Наиболее просто синтез последовательного корректирующего устройства можно произвести по ЛАЧХ. Для этого необходимо использовать ЛАЧХ нескорректированной САУ Gнескорр(w) и желаемую ЛАЧХ, Gскорр(w) соответствующую заданному переходному процессу. ЛАЧХ Gскорр(w) получают с помощью частотного критерия качества, иллюстрированного приведенными выше графиками (см. рис.11.7, рис.11.8).
При последовательном соединении звеньев справедливо соотношение
Wскорр(р)= Wнескорр(р)Wку(р),
где Wку(р) - передаточная функция синтезируемого последовательного корректирующего устройства.
Следовательно
Wку(р)= Wскорр(р)/ Wнескорр(р).
Перейдем к частотной форме записи, используя логарифмические единицы:
20lg| Wку(р)(jw)|=20lg| Wcкорр.(jw)|-20lg| Wнескорр.(jw)|;
Gку(w)=Gскорр.(w) - Gнескорр.(w).
Тип и параметры последовательного корректирующего устройства получают следующим образом:
1) графически вычитают из желаемой ЛАЧХ ординаты ЛАЧХ исходной системы;
2) упрощают ЛАЧХ корректирующего устройства, сравнивают с ЛАЧХ имеющихся в справочных данных типовых корректирующих звеньев и выбирают конкретную схему корректирующего звена;
3) находят по сопрягающим частотам параметры схемы корректирующего устройства.
Более подробно синтез КУ в следующей лекции
Последовательные корректирующие устройства вводятся в цепьрегулятора последовательно с другими звеньями. На рис.8.2 представлена структурная схема системы с последовательным корректирующим устройством.
Рис. 8.2. Структурная схема системы с последовательным корректирующим устройством
Здесь W1(s), W2(s) представляют собой передаточные функции заданных частей регулятора, WПКУ(s) - передаточная функция последовательного корректирующего звена, WОУ(s) - передаточная функция объекта управления.
Передаточная функция регулятора с последовательным корректирующим устройством WR1(s) = W1(s) W2(s) WПКУ(s).
Способ коррекции с помощью последовательного корректирующего устройства не требует сложных расчетов и прост в практическом исполнении. Поэтому он нашел широкое применение, особенно при коррекции систем, в которых используется электрический сигнал в виде напряжения постоянного тока, величина которого функционально связана с сигналом рассогласования. Однако, последовательные корректирующие устройства не ослабляют влияния изменений параметров элементом системы на ее показатели качества. Поэтому последовательные корректирующие устройства рекомендуется применять в системах, в которых элементы имеют достаточно стабильные параметры.
Поиск по сайту: