АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Идеальное дифференцирующие звено

Читайте также:
  1. II звено эпидемического процесса – механизм передачи возбудителей.
  2. Апериодическое звено
  3. Апериодическое звено второго порядка.
  4. Безынерционное (пропорциональное, усилительное) звено
  5. Буксирный трос; 2 – якорная скоба; 3 – удлиненное звено; 4 – якорная цепь; 5 – скоба; 6 – стальной трос (свистов); 7 – стопора якорной цепи.
  6. Буксирный трос; 2 – якорная скоба; 3 – удлиненное звено; 4 – якорная цепь; 5 – скоба; 6 – стальной трос (свистов); 7 – стопора якорной цепи.
  7. Высшее звено управления
  8. Глава 5. ОСНОВНОЕ ЗВЕНО ГРАЖДАНСКИХ СУДОВ ОБЩЕЙ ЮРИСДИКЦИИ
  9. Глава 6. Среднее звено гражданских судов общей юрисдикции
  10. Глава 6. СРЕДНЕЕ ЗВЕНО ГРАЖДАНСКИХ СУДОВ ОБЩЕЙ ЮРИСДИКЦИИ
  11. Государственный бюджет как центральное звено финансовой системы государства, его доходы и расходы
  12. Две ветви. И еще одно звено

Уравнение: 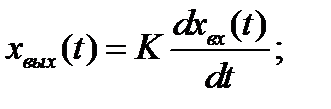- выходная величина пропорциональна скорости изменения входной.

Передаточная функция:

Если хвх и хвых имеют одинаковую размерность, то K измеряется в секундах. В этом случае его принято обозначать T и называть постоянной времени дифференцирующего звена.

АФЧХ:

АЧХ:

ЛАЧХ:

 

Рис. 4.3. Характеристики идеального дифференцирующего звена

Принцип построения ЛАЧХ аналогичен интегрирующему.

По свойствам дифференцирующее звено обратного интегрирующему.

Идеальность обусловлена стремлением А(ω)→∞ при ω→∞.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)