Неединичные обратные связи

Неединичные главные обратные связи применяются для уменьшения ошибки от задающего воздействия. Введем в главную обратную связь, которая обычно равняется единице, устройство с передаточной функцией W₀(s) (рис.10.4).

Рис. 10.4. Структурная схема системы с неединичной главной обратной связью

В этом случае передаточная функция замкнутой системы по задающему воздействию примет вид

(10.10)

Для получения полной инвариантности необходимо выполнить условие Y=G, иначе Фg(s)=1. Отсюда требуемая передаточная функция главной обратной связи должна быть

(10.11)

При разложении этого выражения в степенной ряд получим

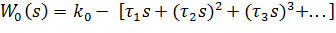
(10.12)

Отсюда видно, что для получения полной инвариантности необходимо использовать главную обратную связь с коэффициентом передачи ko, в общем случае отличном от единицы, и дополнительно ввести положительные обратные связи по производным от управляемой величины. Это условие можно выполнить практически только приближенно. Однако при таком способе, как видно из передаточной функции замкнутой системы, существенно меняется ее характеристическое уравнение. Поэтому одновременно требуется принимать дополнительные меры для того, чтобы получить желаемое качество переходного процесса.

В установившемся режиме (s=0) из (7.11) в системе без астатизма имеем

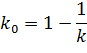
(10.13)

где k = W(0).

Следовательно, если ввести в главную обратную связь системы коэффициент передачи k₀ согласно (10.12), то система будет иметь нулевую установившуюся ошибку от задающего воздействия без введения интегрирующего звена.

Поиск по сайту: