Метод переменных состояния

Метод переменных состояния (МПС) основывается на понятии «состояние системы», которое может быть описано набором физических переменных . Переменные характеризуют состояние системы в следующий момент времени, если известно текущее состояние и приложенные к системе возмущения.

Если –начальный момент времени, то состояние САУ при описывается системой уравнений:

, где:

– набор задающих воздействий для соответствующего состояния .

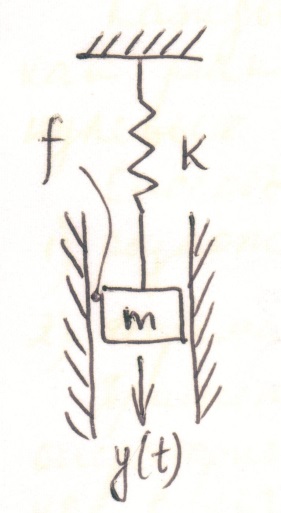Рассмотрим пример:

; (1)

Введем переменные состояния: текущее положение груза и скорость его перемещения . Таким образом:

;

Тогда запишем уравнение (1) в переменных состояниях:

или в форме Коши: .

В общем виде для системы n-го порядка система уравнений в переменных состояния выглядит следующим образом:

Полученную систему удобнее представить в матричной форме:

, где:

– вектор состояния;

– вектор входных переменных;

– квадратная матрица системы;

– матрица уравнения.

Для полного описания САУ уравнение необходимо дополнить еще одним матричным уравнением, связывающим выходные переменные с текущим состоянием:

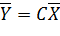, где:

– вектор выходных переменных;

– матрица выходов.

Таким образом для описания САУ в переменных состояния имеем два уравнения:

.

Решением (2) будет выражение вида:

, где:

– матрица Грина, фундаментальная матрица, переходная матрица.

Каждый из элементов матрицы Грина можно рассматривать как реакцию -ой переменной состояния при и нулевых начальных значениях всех остальных .

Способы вычисления матрицы Грина:

1. Разложение в ряд: , где I – един.матрица.

2. Теорема Сильвестра, дающая аналитическое (точное) решение.

Применяя к (2), (3) преобразования Лапласа, получим операторное уравнение САУ в переменных состояния, записанных в матричной форме:

;

Отношение – матричная передаточная функция.

Развитие МПС показало ограниченность классического способа описания САУ «вход-выход». Это связано с моментами наблюдаемости и управляемости.

Управлять можно , наблюдать состояние САУ – измеряя . Можно ли ?Или ?

– неуправляема;

– ненаблюдаема.

САУ называется полностью управляемой, если для любых и и любых и существует , , переводящее САУ .

САУ называется наблюдаемой, если по данным измерения и на конечном интервале можно однозначно определить .

САУ полностью наблюдаема, если наблюдаемы все ее состояния в произвольные моменты времени.

МПС и понятия наблюдаемости и управляемости легли в основу модального управления.

Поиск по сайту: