Соединение элементов

Задача анализа и синтеза САУ упрощается, если известна информация об отдельных элементах и их взаимосвязях.

В САУ элементы соединяются тремя способами:

– последовательно: соединение, при котором выход каждого предыдущего элемента служит входом для каждого следующего.

– параллельно: соединение, при котором на выходы двух или более элементов подается одна и та же величина, а выходы элементов суммируются.

– посредством ОС: соединение, при котором один элемент охватывается обратной связью, содержащей другой элемент.

Определим эквивалентные передаточные функции для перечисленных способов соединений.

Последовательное: (рис.3.1)

Рис. 3.1. Последовательное соединение элементов

Параллельное: (рис.3.2)

Рис. 3.2. Параллельное соединение элементов

Посредством ОС: (рис.3.3)

Рис. 3.3. Соединение элементов посредством ОС.

Эквивалентная передаточная функция САУ с двумя входами. (рис.3.4)

Рис. 3.4. Соединение элементов с двумя входами

Используется принцип суперпозиции, в соответствии с которыми общая САУ на g и z рассматривается в виде суммы:

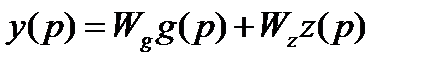
W_g(p) – передаточная функция САУ по задающему воздействию при отсутствии возмущений (z = 0).

W_z(p) – передаточная функция САУ по задающему воздействию при отсутствии задания (g = 0).

Это можно представить следующими структурными схемами: (рис.3.5-3.6)

Рис. 3.5. Соединение элементов при отсутствии возмущений (z = 0)

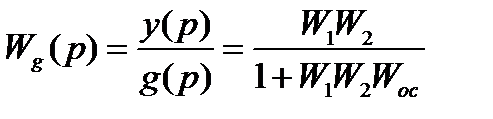
Рис. 3.6. Соединение элементов при отсутствии задания (g = 0)

В итоге:

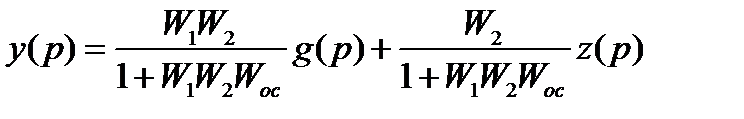
Приведенные эквивалентные передаточные функции справедливы и для статического режима. Поскольку в статическом режиме все производные нулевые, то полагая р = 0 в передаточных функциях элементов переходят к коэффициентам передачи.

Например:

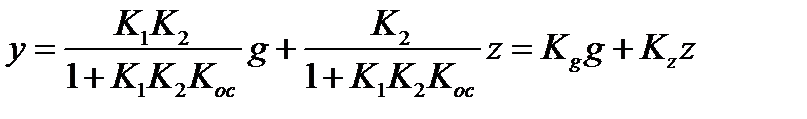, где

К_g – коэффициент передачи САУ по задающему воздействию при отсутствии возмущений.

К_z – коэффициент передачи САУ по возмущающему воздействию при нулевом задании.

Поиск по сайту: