Общее управление динамики для звеньев второго порядка

В общем случае описываются уравнением:

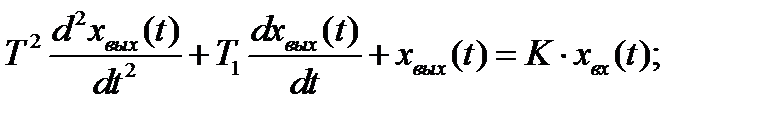
Передаточная функция:

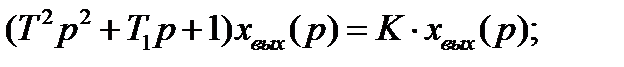
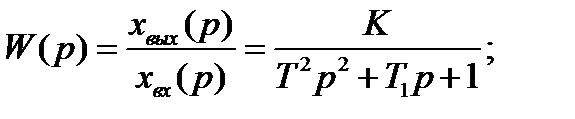
Чаще применяется другой вид записи W(p):

, где 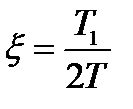- коэффициент демпфирования.

Т.о. звенья второго порядка характеризуются тремя параметрами: K, T, ξ. В зависимости от величины ξ различают типы звеньев второго порядка:

1) 0< ξ <1 – колебательное звено (T₁<2T);

2) ξ =0 – консервативное (T₁=0);

3) ξ ≥ 1 – апериодическое второго порядка (T₁ ≥ 2T);

Рассмотрим свойства звеньев по порядку:

Колебательное:

АФЧХ: 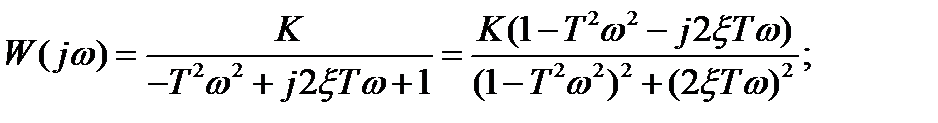где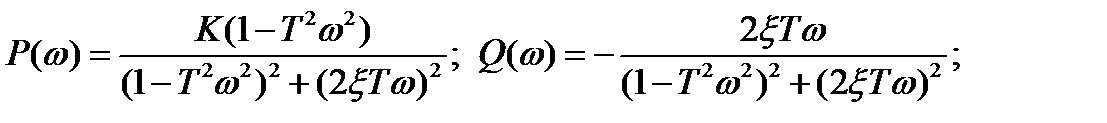

АЧХ: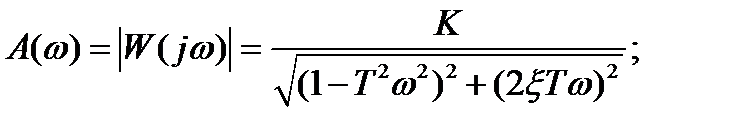

ФЧХ: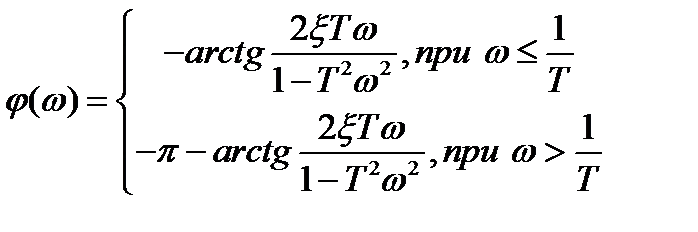

ЛАЧХ: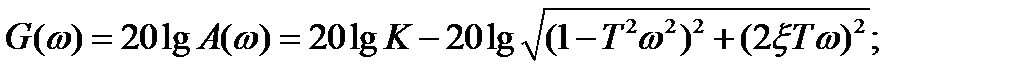

Определим наклон ЛАЧХ при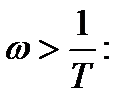

В области НЧ: и

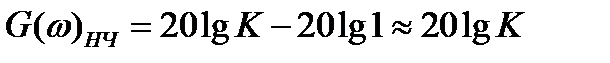
В области ВЧ: 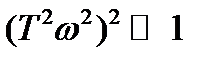и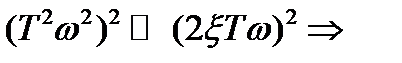

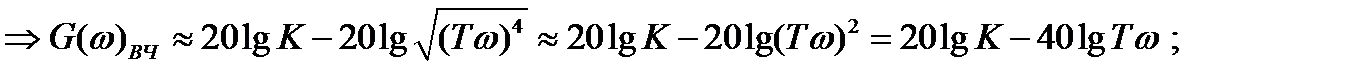Т.о. наклон ЛАЧХ, начинается с равен - 40дБ/дек

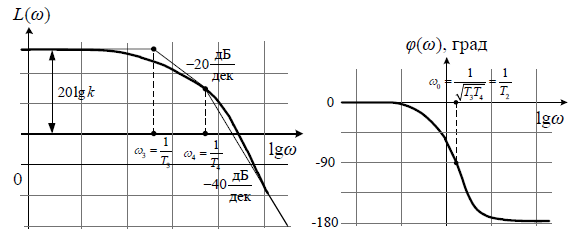
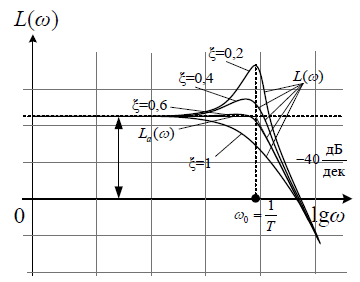
Точная ЛАЧХ отличается от линеаризованной. Считаем, что максимальная ошибка будет в районе ω_с. Тогда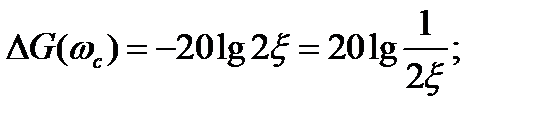

Выводы: При ξ < 0,7 имеет место резонанс и звено колебательное; при

ξ < 0,7 резонанс отсутствует и звено апериодическое 2 ^го порядка.

При ξ ≤ 0,4 использовать линеаризованную ЛАЧХ нельзя!

Т.к. ошибка довольно существенна и больше 3дБ.

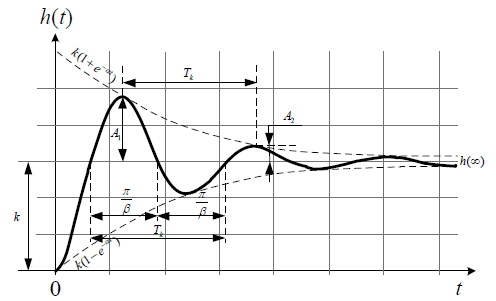
Пример звена:

1) колебательный контур

2) фильтр второго порядка.

Поиск по сайту: