 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение типового примера. Пример 1.1. Решить систему уравнений:
Пример 1.1. Решить систему уравнений:
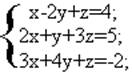
Решение.
а)По формуле Крамера:
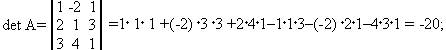


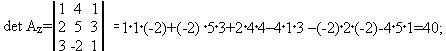
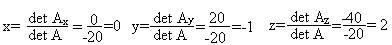
б)Метод Гаусса:
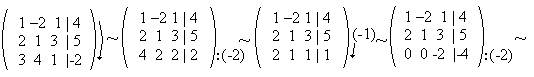
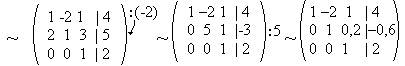
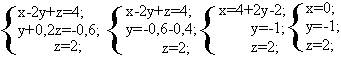
Ответ: x=0; y=-1; z=2;
в)Матричный способ:
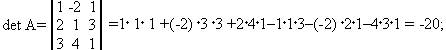
А11=1(1  1–3
1–3  4)=-11 А12=-1(2
4)=-11 А12=-1(2  1–3
1–3  3)=7 А13=1(2
3)=7 А13=1(2  4–3
4–3  1)=5
1)=5
А21=-1(-2  1–1
1–1  4)=6 А22=1(1
4)=6 А22=1(1  1–1
1–1  3)=-2 А23=-1(1
3)=-2 А23=-1(1  4+2
4+2  3)=-10
3)=-10
А31=1(-2  3–1
3–1  1)=-7 А32=-1(1
1)=-7 А32=-1(1  3–1
3–1  2)=-1 А33=1(1
2)=-1 А33=1(1  1+2
1+2  2)=5
2)=5
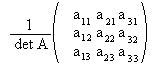
А-1=
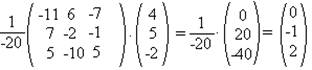
А-1=
Ответ: x=0; y=-1; z=2;
Задачи контрольной работы
В задачах 1.1- 1.20 решить заданную систему линейных уравнений:
· пользуясь формулами Крамера;
· методом Гаусса;
· матричным методом;
1. 1  1.2
1.2 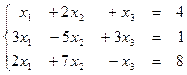
1.3 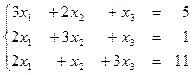 1.4
1.4 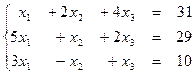
1.5  1. 6
1. 6 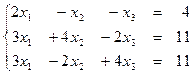
1.7  1.8
1.8 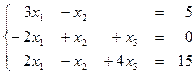
1. 9 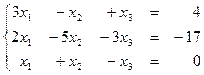 1.10
1.10 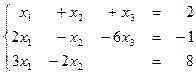
1.11  1.12
1.12 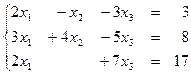
1.13  1.14
1.14 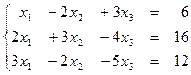
1.15  1.16
1.16 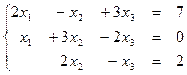
1.17  1.18
1.18 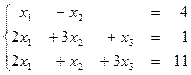
1.19  1.20
1.20 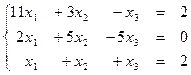
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Поиск по сайту: