Решение типового примера. Даны координаты точек . Пусть

Пример 2.1.

Даны координаты точек . Пусть .

Требуется:

1) записать векторы и в системе орт и найти длины этих векторов;

2) найти орт вектора ;

3) изобразить векторы и в координатной плоскости ;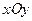

4) найти вектора и аналитически и геометрически.

Решение.

1) Известно, что произвольный вектор представляется в системе орт , по формуле:

, (1)

где – координаты вектора в системе координат .

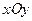Если заданы точки , , то для вектора =

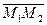
, (2)

Воспользовавшись (2) и координатами точек , получим:

или . Тогда .

или . Тогда .

Если вектор задан своими координатами, то его длина (модуль) вычисляется по формуле:

(3)

Используя формулу (3), получаем длины векторов и :

,

.

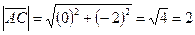2) Известно, что орт вектора можно найти по формуле:

, т.е. , (4)

Воспользовавшись формулами (4), получим: .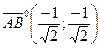

3) Найдем векторы и аналитически.

.

Таким образом, .

.

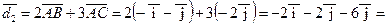
Таким образом, (рис.1).

Найдем векторы и геометрически (рис.2).

Поиск по сайту: