АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение типового примера. Пример 9.4. Исследовать на экстремум функцию

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  7. Аналитическое решение
  8. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  9. Арбитражное разрешение международных споров в Древней Греции
  10. Арбитражное разрешение международных споров в Древнем Риме
  11. Б) Правовое разрешение конфликтов
  12. В результате получаем общее решение системы

 

Пример 9.4. Исследовать на экстремум функцию .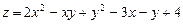

 

Решение. В соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

Для этого находим частные производные функции:

; ,

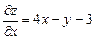затем приравниваем их к нулю и решаем систему уравнений:

откуда находим 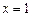, . Таким образом, получили точку , в которой будем продолжать исследовать функцию на экстремум.

Находим значения частных производных второго порядка в точке :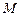

; ; .

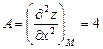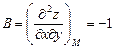Найдем знак дискриминанта в указанной точке:

.

Так как дискриминант больше нуля > 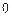и > 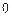, то функция имеет минимум в точке :

.

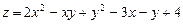Ответ. В точке функция имеет минимум .


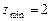1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)