 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение. При непосредственной подстановке получаем неопределенность:
а)  .
.
При непосредственной подстановке получаем неопределенность:
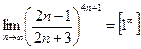 .
.
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел  . Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины:
. Для этого представим основание в виде суммы единицы и некоторой бесконечно малой величины:
 .
.
Т.о. наш предел примет вид:
 .
.
Введем такую новую переменную  , что
, что 
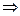
 ,
,  или
или  . При
. При  переменная
переменная  . Показатель степени примет вид:
. Показатель степени примет вид:
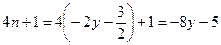 .
.
Таким образом, пользуясь свойствами пределов и правилами действия со степенями, будем иметь:


 .
.
б)  .
.
При непосредственной подстановке получаем неопределенность:
 .
.
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел  . Для этого положим
. Для этого положим  , или
, или 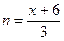 ,
,  , тогда показатель степени примет вид:
, тогда показатель степени примет вид:  . При
. При  ,
,  .
.
Выразив основание и показатель степени через  , а также воспользовавшись свойствами пределов и правилами действия со степенями, получим
, а также воспользовавшись свойствами пределов и правилами действия со степенями, получим
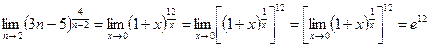 .
.
в)  .
.
При непосредственной подстановке получаем неопределенность:
 .
.
В данном случае для освобождения от неопределенности будем использовать второй замечательный предел  . Преобразуем выражение, стоящее в скобках. Для этого представим основание в виде суммы единицы и некоторой дроби:
. Преобразуем выражение, стоящее в скобках. Для этого представим основание в виде суммы единицы и некоторой дроби:

 .
.
Поиск по сайту: