АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение типового примера. Пример 9.3. Найти градиент функции в точке и его длину

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  7. Аналитическое решение
  8. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  9. Арбитражное разрешение международных споров в Древней Греции
  10. Арбитражное разрешение международных споров в Древнем Риме
  11. Б) Правовое разрешение конфликтов
  12. В результате получаем общее решение системы

Пример 9.3. Найти градиент функции в точке и его длину.

Решение. Градиент функции в точке вычисляется по формуле:

.

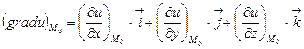Сначала найдем все частные производные первого порядка от заданной функции:

; ; .

 

Далее вычислим значения этих частных производных первого порядка в точке :

,

,

.

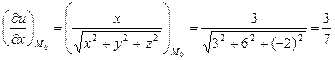Подставляя найденные значения в формулу градиента, получаем:

.

Находим его длину:

.

Ответ. Градиент функции в точке равен , длина .

Задачи контрольной работы

В заданиях 3.1-3.20 найти градиент функции в заданной точке и его длину.

 

9.3.1. , . 9.3.2. , .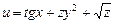

9.3.3. 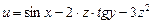, . 9. 3.4. , .

9.3.5. , . 9.3.6. , .

9.3.7. , 9.3.8. , .

9.3.9. , . 9.3.10. , .

9.3.11. , . 9.3.12. , .

9.3.13. , 9.3.14. , .

9.3.15. 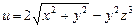, . 9.3.16. , .

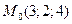9.3.17. 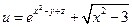, . 9.3.18. , .

9.3.19. , . 9.3.20. , .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)