АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение. 1) Составим интервальный ряд для признака Х

Читайте также:
  1. Волновое уравнение для упругих волн и его общее решение.
  2. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  3. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
  4. Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
  5. Рациональное управленческое решение. Способы принятия рационального решения. Списки. Дерево решений. Причинно-следственные диаграммы.
  6. РЕШЕНИЕ.
  7. Решение.
  8. Решение.
  9. Решение.
  10. Решение.
  11. Решение.
  12. Решение.

1) Составим интервальный ряд для признака Х. Для этого найдём размах варьирования значений признака по формуле: RХ =Xmax - Xmin.

Из таблицы 13.1 следует: Xmax = 68; Xmin = 18 и RХ = 68 - 18 = 50.

Число интервалов m, на которые следует разбить интервал значений признака, найдём по формуле Стерджеса: m = 1+3,322 lg n, где n - объём выборки, то есть число единиц наблюдения.

В нашем примере n =60. Получим: m = 1+3,322• lg 60 = 1+3,322•1,778 = =6,9 ≈7.

 

Теперь рассчитаем шаг (длину частичного интервала) h по формуле:

h = 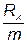= 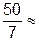7,1. Округление шага производится, как правило, в большую сторону. Таким образом, принимаем h =8.

За начало первого интервала принимаем такое значение из интервала [ х min- 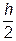; х min), чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём х min - 2 = 18 - 2 = 16. В результате получим следующие границы интервалов: 16-24-32-40-48-56-64-72.

Подсчитаем частоту каждого интервала, то есть число вариант, попавших в этот интервал. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал.

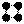
Для удобства подсчёта частот используют «метод конверта»:

Его вершины, стороны и диагонали обозначают одну единицу. Итого: 4 вершины, 4 стороны и 2 диагонали. Всего 10 единиц. Например,

2; -7; - 8; - 10.

Таблица 13.2


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)