Пример 3.1

Даны координаты вершин треугольника ABC: A (4; 3), B (16; - 6), C (20; 16). Найти

1) длину стороны АВ:

Расстояние d между двумя точками M ₁ (x₁; у₁) и M₂(x₂; y₂) на плоскости определяется формулой

(1)

Применяя (1), находим длину стороны АВ:

2) уравнения сторон АВ и ВС и их угловые коэффициенты:

Уравнение

(2)

является уравнением прямой, проходящей через две точки

М₁ (x₁; y ₁) и M ₂(x₂ ; у₂)

Подставляя в (2) координаты точек A и B, получим уравнение прямой АВ:

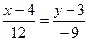; ; 4 y -12=-3 x +12; или 3 x +4 y -24=0 (АВ).

Уравнение

y = kx + b

называется уравнением прямой с угловым коэффициентом; k — угло­вой коэффициент, b — величина отрезка, ко­торый отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением Ах+Ву+С=0, то её угловой коэффициент определяется по формуле k =

Решив последнее уравнение относительно y, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:

4 y =-3 x+ 24, или y = - x+ 6, откуда k _АВ =

Аналогичным образом, подставляя координаты точек B и C в (2), находим уравнение прямой BC: 11 x- 2y -188=0 (ВС) откуда k _ВС =

3) угол B:

Если известны угловые коэффициенты двух прямых k₁ и k₂, то один из углов φ между этими прямыми определяется по формуле

(3)

Искомый угол В образован прямыми АВ и BC, угловые коэффициенты которых известны из предыдущего пункта. Применяя (3), получим

= 2.

4) уравнение медианы АЕ:

Определим координаты точки Е, которая является серединой отрезка BC по формулам координат середины данного отрезка:

, (4)

Имеем для точки Е: ,
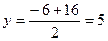
Таким образом, Е (18; 5).

Подставляя в (2) координаты точек А и Е, находим уравнение медианы АЕ:

; ; x- 7 y +17=0 (АЕ).

5) уравнение и длину высоты СД:

Уравнение

у — y₀ = k(x—х₀) (5)

является уравнением прямой, которая проходит через точку М₀ (х₀ ; у₀) и имеет угловой коэффициент k.

Высота СД перпендикулярна стороне АВ. Воспользуемся условием перпендикулярности 2 – х прямых на плоскости. Признаком перпендикулярности двух прямых является соотношение

k₁k₂ = —1 или k₂ = —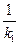

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. Отсюда

k_CD = — =

Подставив в (5) координаты точки С и k_CD получим уравнение высоты СD:

у — 16 = (x —20); 4 x-3y -32=0 (СD).

Для нахождения длины высоты СD определим координаты точки D как точки пересечения прямых АВ и СD, решив совместно систему уравнений, их задающих:

Откуда x = 8, y = 0, т.е. D (8; 0).

6) уравнение окружности, для которой высота СD есть диаметр;

Уравнение окружности с центром в точке О(а; b) радиуса R имеет вид:

(x-a)²+(y-b)²=R² (6)

Если СD есть диаметр, то центр окружности – точка О – есть середина СD. Используя формулы (4) имеем для О:

, ,

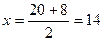Таким образом, О (14; 8).

Если СD есть диаметр, то радиус окружности – есть отрезок СО. Используя (1) найдем радиус:

R=

Тогда, (x- 14 ) ² +(y- 8 ) ² =80 – уравнение искомой окружности.

7) уравнение прямой, проходящей через точку Е параллельно стороне

АВ, и точку K ее пересечения с высотой СD:

Т.к. заданная прямая параллельна стороне АВ, то можем использовать условие параллельности 2 – х прямых на плоскости: Признаком параллельности двух прямых является равенство их угловых коэффициентов

k₁ = k₂,

т.е. k = k_AB = -3/4. Знаем, что прямая проходит через точку Е с заданным угловым коэффициентом. Можем использовать уравнение (5):

у — 5 = -3/4(x —18); 4 у — 20 = -3 (x— 18); 3 x +4 у - 2 = 0. (EL)

Точку K пересечения EL с высотой СD найдем, решив совместно систему уравнений, задающих эти прямые:

Откуда, x = 8, y = -88/25, т.е. K (8; -88/25).

8) систему линейных неравенств, определяющих треугольник АВС:

Используя неравенство треугольника (сумма двух любых сторон треугольника меньше третьей его стороны), получаем систему:

Из п. 2 известны 3 x +4 y -24=0 (АВ), 11 x- 2y -188=0 (ВС). Запишем уравнение АС, используя (2):

; ; 13(x -4)=16(y -3); 13 x -16 y -4=0 (АС).

Тогда, система линейных неравенств, определяющих треугольник АВС примет вид:

Или

Поиск по сайту: