АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определенный интеграл

Читайте также:
  1. Б. Осознание предпочитаемой сферы жизнедеятельности («неопределенный рассказ»)
  2. Вставьте определенный, неопределенный или нулевой артикль. Выполните это упражнение письменно. В случае сомнений обратитесь к правилам.
  3. Лишение свободы на определенный срок, как вид основного наказания. Порядок и условия назначения. Отличие от ограничения свободы.
  4. Лишение свободы на определенный срок. Виды и порядок назначения исправительных учреждений
  5. Неопределенный артикль a (an)
  6. Неопределенный и определенный интегралы.
  7. Неопределенный и определенный интегралы.
  8. Неопределенный интеграл
  9. Определенный интеграл
  10. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
  11. Первообразная и неопределенный интеграл

Связь определенного и неопределенного интегралов задается формулой Ньютона – Лейбница:

т. е. определенный интеграл от непрерывной функции f (x) равен приращению первообразной функции F(x) на отрезке [a, b].

Формула Ньютона – Лейбница позволяет вычислять определенный интеграл, используя методы вычисления неопределенного интеграла, рассмотренные в предыдущей главе.

Пример 8.8. Вычислить интеграл

Решение. Используя свойства определенного интеграла и формулу Ньютона – Лейбница, получим:

Пример 8.9. Вычислить интеграл

Решение. Полагая имеем 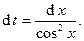Найдем новые пределы интегрирования:

Имеем:

Пример 8.10. Вычислить интеграл

Решение. Применяя формулу интегрирования по частям, для определенного интеграла

найдем:

 

= =

 

=


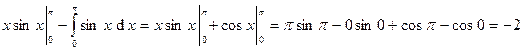
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)