 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Допускающие понижение порядка
I. Уравнения вида y′′ = f(x)
решается последовательным двукратным интегрированием. При каждом интегрировании получается одна произвольная постоянная, а общее решение содержит две константы.
Пример 10. 5. Найти общее решение дифференциального уравнения
y''=sin3x.
Решение. Последовательно интегрируя данное уравнение, получим
.
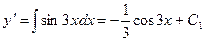
II. Уравнение второго порядка, не содержащее искомой функции
Уравнение вида F(x, y', y'') = 0 допускает понижение порядка введением новой функции, следующим образом y'= p(x), тогда y''= p'(x).
Пример 10.6. Найти общее решение дифференциального уравнения
.
Решение. Данное уравнение не содержит функции у, поэтому положим
y'= p(x), тогда y''= p'(x) и уравнение примет вид:
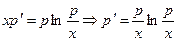
Получили однородное уравнение первого порядка. Для его решения воспользуемся подстановкой p=ux, тогда p'= u'x+u и, следовательно, приходим к уравнению
откуда 
.
Возвращаясь к функции у, получаем общее решение
или 
.
Это уравнение с разделяющимися переменными
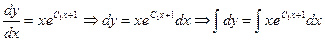
Интеграл, стоящий в правой части уравнения интегрируем по частям:
= 
.
Окончательно получаем: 
.
III. Уравнения второго порядка, не содержащие независимой переменной
Уравнение F(y, y', y'') = 0 при помощи подстановки y'= p(y) уравнение сводиться к уравнению первого порядка
F(y, p, p 
) = 0.
Пример 10.7. Найти частное решение дифференциального уравнения
2yy'3+y''=0, удовлетворяющее начальным условиям y(0)=0, y'(0)=-3.
Решение. Это уравнение не содержит независимой переменно, следовательно, будем его решать, полагая y'= p(y), откуда 
. Используя данные подстановки преобразуем данное уравнение к виду
.
Интегрируя, получим 
.
Получили дифференциальное уравнение первого порядка
, (*)
Решая которое получим: 
.
Итак, общий интеграл дифференциального уравнения имеет вид:
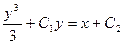
Найдем частный интеграл, для этого в общий интеграл и в уравнение (*) подставим начальные условия y(0)=0, y'(0)=-3. Получаем систему двух уравнений для определения постоянных С1 и С2.
.
Таким образом, искомое частное решение имеет вид y3 – y= 3x.
Поиск по сайту: