АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Однородные уравнения. Уравнения вида называется однородным дифференциальным уравнением первого порядка

Читайте также:
  1. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  2. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  3. Геометрические преобразования точек и отрезков. Однородные координаты
  4. Инфраструктура информационного рынка - совокупность секторов, каждый из которых объединяет группу людей или организаций, предлагающих однородные информационные продукты и услуги.
  5. Линейные неоднородные дифференциальные уравнения
  6. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
  7. Линейные неоднородные дифференциальные уравнения с постоянными
  8. Линейные однородные дифференциальные уравнения в частных
  9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
  10. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
  11. Линейные однородные дифференциальные уравнения с
  12. Линейные однородные дифференциальные уравнения с

Уравнения вида называется однородным дифференциальным уравнением первого порядка.

Однородное уравнение приводиться к уравнению с разделяющимися переменными подстановкой y=u∙x, где u=u(x) - новая искомая функция. Заменим у и y'= u'x + u в данном уравнении:

u'x + u = f(u)

Разделив переменные, получаем:

Проинтегрировав, полученное уравнение найдем общее решение или общий интеграл.

Пример 10.3. Найти общее решение дифференциального уравнения

.

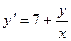Решение. Введем новую функцию , тогда и 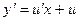. Заменяя в исходном уравнении функцию у и ее производную у' получим уравнение с разделяющимися переменными:

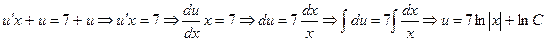
u = lnCx7.

Возвращаемся к старой функции .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)