Решение типового примера. Пример 3.2. Определить вид кривой, построить, найти координаты фокусов и эксцентриситет:

Пример 3.2. Определить вид кривой, построить, найти координаты фокусов и эксцентриситет:

Пусть дана кривая .

Решение:

Приведем данное уравнение к каноническому виду. Для этого сгруппируем отдельно члены, содержащие переменные и :

.

В каждой из скобок вынесем коэффициент при квадрате переменной, а затем выделим полный квадрат, используя формулы сокращенного умножения :

.

Первые три слагаемые в скобках образуют полный квадрат разности , следовательно

.

Аналогичные действия осуществим для переменной :

.

Первые три слагаемые в скобках образуют полный квадрат суммы , следовательно

.

Тогда исходное уравнение примет вид:

,

,

.

Введем обозначения: . Произведенную замену будем рассматривать, как преобразование декартовых координат в координаты при параллельном сдвиге координатных осей. Причем новое начало координат находится в точке . В этой системе координат наше уравнение примет вид:

.

Это каноническое уравнение эллипса. Его полуоси . Кроме того, 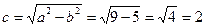, следовательно эксцентриситет . остается найти координаты вершин и фокусов эллипса. В новой системе координаты вершин таковы: ; координаты фокусов . Так как старые координаты выражаются через новые по формулам , то, возвращаясь к первоначальной системе координат получим: , .

3.2.1	3.2.2
3.2.3	3.2.4
3.2.5	3.2.6
3.2.7	3.2.8
3.2.9	3.2.10
3.2.11	3.2.12
3.2.13	3.2.14
3.2.15	3.2.16
3.2.17	3.2.18
3.2.19	3.2.20

Поиск по сайту: