Решение типового примера. Пример 14.1. Требуется решить задачу линейного программирования графическим методом:

Пример 14.1. Требуется решить задачу линейного программирования графическим методом:

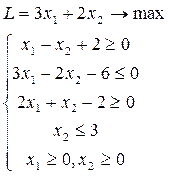
Решение. Построим сначала область допустимых решений, которая представляет собой множество решений системы линейных ограничений.

Графически решение каждого неравенства есть одна из полуплоскостей, на которые прямая линия ax +by =c делит координатную плоскость. Решением системы неравенств будет выпуклый многоугольник, представляющий собой пересечение полуплоскостей – решений каждого неравенства.

Пронумеруем каждое неравенство и решим его (см. рис.1.1)

1.

Построим прямую , для чего найдём координаты двух её точек, например, (0; 2) и (2; 4). Чтобы выбрать полуплоскость-решение для данного неравенства, подставим в это неравенство координаты любой точки, не лежащей на построенной прямой, например точки с координатами (0; 0). Получаем 0 – 0 +2 0. Это верное неравенство. Следовательно, полуплоскость, содержащая эту точку, будет являться решением неравенства 1. Стрелками отметим решение.

Аналогично строим решения каждого неравенства.

2.

Строим прямую 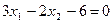, проходящую через точки с координатами (0;-3) и (2;0). Решением неравенства является полуплоскость, содержащая начало координат (0,0), так как: 3∙0 –2∙ 0 – 6 0 - верное неравенство.

3.

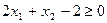
Строим прямую , проходящую через точки с координатами (0;2) и (1;0). Затем в неравенство подставляем координаты точки (0;0): 2∙0 + 0 – 2 0. Так как это неравенство неверное, то решением является полуплоскость, не содержащая точку с координатами (0;0).

4.

Прямая, определяемая уравнением проходит через точку (0;3) параллельно оси абсцисс. Полуплоскость, лежащая ниже этой прямой и есть решение данного неравенства.

Два последних неравенства определяют первый квадрант координатной плоскости.

На рис. 14.1 многоугольник ABCDE представляет собой область допустимых решений задачи линейного программирования.

Рис. 14. 1. Решение задачи линейного программирования.

Для нахождения оптимального решения построим вектор (3;2), координаты которого равны коэффициентам при переменных в целевой функции L. Этот вектор является нормальным вектором для линий уровня L=const, а также одну из линий уровня, например, . Так, как задача на отыскание максимального значения целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой, то есть такой линии уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей. Эта прямая проходит через точку С пересечения прямых 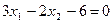и , для определения координат точки С решим систему уравнений , получаем С(4;3) в этой точке целевая функция достигает максимума .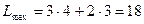

Ответ: при Х*= (4;3).

Поиск по сайту: