 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи контрольной работы. В задачах 10.1- 10.20 решить дифференциальные уравнения первого порядка
В задачах 10.1- 10.20 решить дифференциальные уравнения первого порядка.
10.1. 
; 10. 2. 
; 10.3. 
;
10.4.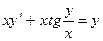 
; 10. 5. 
; 10.6. 
;
10.7. 
; 10.8. 
; 10.9.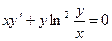 
;
10.10. 
; 10.11. 
; 10.12. 
;
10.13. 
; 10.14. 
; 10.15. 
;
16. 
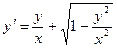; 10.17. 
; 10.18. 
;
10.19. 
; 10.20. 
.
В задачах 10.21 – 10.40 найти частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.
10.21. y'' – 7y' + 10y = 0; y(0) = 2; y'(0) = -1.
10.22. y'' + 2y' + 10y = 0; y(
) = 0; y'() = 1.
10.23. y'' – 6y' + 9y = 0; y(0) = 1; y' (0) = 0.
10.24. y'' + 8y' + 7y = 0; y(0) = 2; y'(0) = 1.
10.25. y'' + 9y = 0; y(π) = 0; y'(π) = -1.
10.26. y'' – 7y' + 12y = 0; y(0) = 2; у'(0)=-2.
10.27. y'' + 9y' = 0; y(0) = 1; y'(0) = -3.
10.28. y'' – 3y' + 2y = 0; y(0) = 0; y'(0) = 1.
10.29. y'' – 5y' + 6y = 0; y(0) = 5; y'(0) = 0.
10.30. y'' – 2y' + 5y = 0; y(0) = -1; y'(0) = 0.
10.31. y'' + 16y = 0; y(π) = -1; y'(π) = 0.
10.32. y'' + 10y' + 25y = 0; y(0) = 1; y'(0) = 1.
10.33. y'' – 6y' = 0; y(0) = 2; y'(0) = -2.
10.34. y'' – 4y' + 4y = 0; y(0) = 1; y'(0) = 3.
10.35. y'' – 8y' + 15y = 0; y(0) = 1; y'(0) = -2.
10.36. y'' – 4y' + 17y = 0; y() = 0; y'() = 1.
10.37. y'' – 2y' + y = 0; y(1) = 0; у'(1)=2
10.38. y'' + y = 0; y(π) = -1; y'(π) = -4.
10.39. y'' – 7y' + 6y = 0; y(0) = 2; y'(0) = 0.
10.40. y'' + 8y' + 16y = 0; y(0) = 1; y'(0) = 0.
В задачах 10.41 – 10.60 найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
10.41. у'' - 2у' = 3х2 + 1 10.51. у'' + 2у' = х2 -3х +1
10.42. у'' - 5у' + 6у = 2хе-х 10.52. у'' - 5у' - 24у = (2х + 3)ех
10.43. у'' + 8у' = (х-1)е2х 10.53. у'' - 2у' - 3у = 8е3х
10.44. у'' - 6у' + 8у = 3е4х 10.54. у'' + 2у' - 3у =- 2е3х
10.45. у'' - 2у' - 3у = хе-х 10.55. у'' + 8у' = (х2+1) е-х
10.46. у'' + у' - 2у = (х = 2)е-2х 10.56. у'' + 4у' + 3у = -хе-х
10.47. у'' + 2у' - 8у = (3х+1)е2х 10.57. у'' - 2у' - 3у =(х + 2)е-х
10.48. у'' + 7у' = 2х2 + х 10.58. у'' + у' + 6у = 2(х – 1)е2х
10.49. у'' - у' = 8х2 ех 10.59. у'' - 4у' = 2х2 – 3х +1
10.50. у'' + 3у' -10у = 2х2ех 10.60. у'' - 5у' + 6у = 2хе3х
Поиск по сайту: