 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение типового примера. Задача 12.5.Для случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета в беспроигрышной лотерее
Задача 12.5. Для случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета в беспроигрышной лотерее, в которой разыгрывается 100 выигрышей (10 по 50 руб., 30 по 10руб., 60 по 1 руб.), 1) построить ряд распределения; 2) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение; 3)найти функцию распределения вероятностей.
Решение. 1) Случайная величина в результате испытания принимает одно из своих возможных значений, которое предугадать заранее невозможно. Дискретная случайная величина Х, принимающая значения х1, х2,…, хn с вероятностями р1, р2,…, рn, может быть задана рядом распределения, который записывается в виде таблицы:
| Х | х1 | х2 | … | хn |
| Р | р1 | р2 | … | рn |
В нашем случае возможные значения случайной величины Х: 1, 10 и 50. Вероятности этих значений  ,
,  ,
,  .
.
Получаем ряд распределения:
| Х | |||
| Р | 0,6 | 0,3 | 0,1 |
2) Так как математическое ожидание М(Х) для дискретной случайной величины Х находится по формуле
 ,
,
то получаем: М(Х) = 1∙0,6 +10∙0,3 + 50∙0,1 = 8,6
Дисперсия D(Х) случайной величины Х может быть найдена по формуле:
D(Х) = М(Х2) - [М(Х)]2
Вычислим М(Х2) = 12∙0,6 + 102∙0,3 + 502∙0,1 = 280,6. Тогда D(Х) = 280,6 – (8,6)2 = 206,64.
Среднее квадратическое отклонение  . Получаем:
. Получаем: 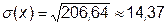 .
.
3) Для случайной величины Х функция распределения вероятносте й F(x) определяется формулой: F (х) = Р (Х<х)
Для дискретной случайной величины F(x) вычисляется по формуле:
 .
.
Найдём функцию распределения вероятностей.
Если x < 1, то F(x)=Р(Х<х)=Р(-¥ <X< x)=0, так как интервал (-¥; х) не содержит возможных значений Х; если 1 < x ≤10, то F(x)=Р(Х<х)= =Р(-¥ <X< x)=P(X=1)=0,6; если 10< x≤50, то F(x)=Р(Х<х)=Р(Х=1)+ Р(Х=10)=0,6+0,3=0,9; если х>50, то F(x)=Р(Х<х)=Р(Х=1)+ Р(Х=10)+Р(Х=50)=0,6+0,3+0,1=1. Итак,

Ответ: 2) М(Х) = 8,6; D(Х) = 206,64.  .
.
Поиск по сайту: