ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕРЯДЫ

Программные вопросы.

1) Сходимость и сумма ряда. Необходимое условие сходи­мости ряда.

2) Теоремы сравнения.

3) Признаки Даламбера и Коши.

4) Интегральный признак сходимости ряда.

5) Теорема Лейбница. Оценка остатка знакочередующегося ряда.

6) Теорема о сходимости абсолютно сходящегося ряда. Свойства абсолютно сходящихся рядов.

7) Понятие равномерной сходимости. Признак Вейерштрасса.

8) Теорема о непрерывности суммы функционального ряда.

9) Теоремы о почленном интегрировании и почленном дифференцировании функционального ряда.

10)Теорема Абеля. Интервал и радиус сходимости степенно­го ряда.

11)Теорема о равномерной сходимости степенного ряда. Непрерывность суммы ряда.

12)Почленное интегрирование и дифференцирование степенных рядов.

13)Разложение функции в степенной ряд. Ряд Тейлора.

14)Разложение по степеням бинома .

15)Условия разложимости функции в ряд Тейлора.

16)Разложение по степеням функций .

Постановка задачи.

Найти сумму ряда , где – целые числа.

План решения задачи.

Суммой ряда называется предел последовательности его частичных сумм 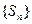, т.е. где .

1. По условию задачи 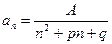.Если корни знаменателя отличаются на целое число, т.е. , где k – натуральное число, то члены последовательности частичных сумм ряда легко найти, т.к. в выражении многие слагаемые взаимно уничтожаются.

2. Раскладываем общий член ряда на элементарные дроби:

3. Находим n-ю частичную сумму ряда: ,сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле .

Замечание 1. Если коэффициент при не равен единице, но равен квадрату целого числа, то все выполняется аналогично.

Замечание 2. Если суммирование ряда начинается не с 1, а с некоторого номера m, то n-я частичная сумма ряда будет .

Задачи с 11.1.1 – 11.1.20. Найти сумму ряда.

11.1.1	11.1.11
11.1.2	11.1.12
11.1.3	11.1.13
11.1.4	11.1.14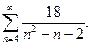
11.1.5	11.1.15
11.1.6	11.1.16
11.1.7	11.1.17
11.1.8	11.1.18
11.1.9	11.1.19
11.1.10	11.1.20

Постановка задач.

Исследовать сходимость ряда с неотрицательными членами , где и – функции с известными наименьшими и наибольшими значениями, причем функция монотонно зависит от

План решения задач.

1. Проверяем, что , т.к. если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Поскольку 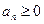, то можно применить первую теорему сравнения:

Пусть даны два ряда с неотрицательными членами и .Если , то из сходимости ряда следует сходимость ряда

Если , то из расходимости ряда следует расходимость ряда

3. Чтобы сделать вывод о сходимости (расходимости) данного ряда, необходимо установить справедливость одной из двух гипотез:

1) Исходный ряд сходится. 2) Исходный ряд расходится.

3.1.Проверяем первую гипотезу. Чтобы установить, что исходный ряд сходится, нужно найти сходящийся ряд такой, что .

В качестве эталонного ряда используем одни из следующих рядов:

а) сходящийся гармонический ряд при 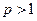(С– константа);

б) сходящийся геометрический ряд при (С– константа).

Если существует сходящийся ряд такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд сходится. В противном случае проверяем вторую гипотезу.

3.2. Проверяем вторую гипотезу. Чтобы установить, что исходный ряд расходится, нужно найти расходящийся ряд такой, что .

В качестве эталонного ряда используем одни из следующих рядов:

а) расходящийся гармонический ряд при (С– константа);

б) расходящийся геометрический ряд при (С – константа).

Если существует расходящийся ряд такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд расходится.

Замечание. Для оценки общего члена ряда используем неравенства:

и т.п.

Задачи 11.2.1-11.2.20. Исследовать на сходимость ряд.

11.2.1.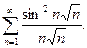

11.2.2.

11.2.3.

11.2.4.

11.2.5.

11.2.6.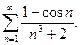

11.2.7.

11.2.8.

11.2.9.

11.2.10.

11.2.11.

11.2.12.

11.2.13.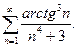

11.2.14.

11.2.15.

11.2.16.

11.2.17.

11.2.18.

11.2.19.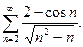

11.2.20.

Задачи 11.3.1-11.3.20. Исследовать на сходимость ряд.

11.3.1

11.3.2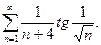

11.3.3

11.3.11

11.3.12

11.4.13

11.3.4

11.3.5

11.3.6

11.3.7

11.3.8

11.3.9

11.3.10

11.3.14

11.3.15

11.3.16

11.3.17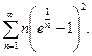

11.3.18

11.3.19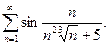

11.3.20

Постановка задачи 4.

Исследовать сходимость ряда с положительными членами где содержит произведения многих сомножителей (например, степени и факториалы).

План решения задачи 4.

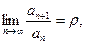Признак Даламбера. Пусть дан ряд с положительными членами Если существует предел то при ряд сходится, а при расходится. Если , то признак Даламбера ответа не дает и требуется дополнительное исследование ряда.

1. Проверяем, что , т.к. если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Проверяем, что для всех .

3. Вычисляем предел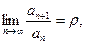

4. Применяем признак Даламбера и делаем вывод о сходимости или расходимости исследуемого ряда.

Замечание. Если общий член исследуемого ряда имеет сложный вид, то в таком случае следует воспользоваться предельным признаком сравнения и применить признак Даламбера к упрощенному ряду.

Задача 4. Исследовать на сходимость ряд.

11.4.1	11.4.11
11.4.2	11.4.12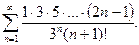
11.4.3	11.4.13
11.4.4	11.4.14
11.4.5	11.4.15
11.4.6	11.4.16
11.4.7	11.4.17
11.4.8	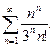11.4.18
11.4.9	11.4.19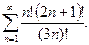
11.4.10	11.4.20

Постановка задачи 5.

Исследовать сходимость ряда с положительными членами и существует и легко вычисляется.

План решения задачи 5.

Радикальный признак Коши. Пусть дан ряд с положительными членами Если существует предел ,то при ряд сходится, а при – расходится. Если , то признак Коши ответа не дает и требуется дополнительное исследование ряда.

1. Проверяем, что , т.к. если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Проверяем, что для всех . 3. Вычисляем предел .

4. Применяем радикальный признак Коши и делаем вывод о сходимости или расходимости исследуемого ряда.

Замечание 1. Если общий член исследуемого ряда имеет сложный вид, то в таком случае следует воспользоваться предельным признаком сравнения и применить радикальный признак Коши к упрощенному ряду.

Замечание 2. Полезно иметь в виду, что ()

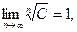Задача 5. Исследовать ряд на сходимость.

11.5.1	11.5.11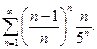
11.5.2	11.5.12
11.5.3	11.5.13
11.5.4	11.5.14
11.5.5	11.5.15
11.5.6	11.5.16
11.5.7	11.5.17
11.5.8	11.5.18
11.5.9	11.5.19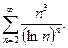
11.5.10	11.5.20

Постановка задачи 6.

Исследовать сходимость ряда с положительными членами , где , причем первообразная функции легко вычисляется.

План решения задачи 6.

Если , причем первообразная функции легко вычисляется, то применяем интегральный признак Коши:

Если функция , принимающая в точках 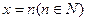значения , убывает в некотором промежутке , , то ряд и несобственный интеграл либо оба сходятся, либо оба расходятся одновременно.

1. Проверяем, что , т.к. если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда.

2. Упрощаем, если требуется, выражение для , т.е. будем исследовать сходимость ряда , такого, что при и выбраны так, чтобы функция имела очевидную первообразную . Затем используем вторую теорему сравнения.

3. Исследуем сходимость несобственного интеграла по определению

.

4. Применяем интегральный признак Коши к ряду и затем делаем вывод о сходимости или расходимости исходного ряда , используя вторую (предельную) теорему сравнения.

Замечание. Интегральный признак Коши применяется, в частности к рядам вида

Задача 6. Исследовать на сходимость ряд.

11.6.1	11.6.11
11.6.2	11.6.12
11.6.3	11.6.13
11.6.4	11.6.14
11.6.5	11.6.15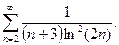
11.6.6	11.6.16
11.6.7	11.6.17
11.6.8	11.6.18
11.6.9	11.6.19
11.6.10	11.6.20

Постановка задачи 7.

Исследовать сходимость знакочередующегося ряда ,

План решения задачи 7.

1. Исследуем сходимость ряда, составленного из модулей, , используя теоремы сравнения и признаки сходимости для рядов с положительными членами.

Если ряд из модулей сходится, то исследуемый знакочередующийся ряд сходится абсолютно.

2. Если ряд из модулей расходится, то остается еще возможность того, что исходный ряд сходится условно. Чтобы исследовать эту возможность, применяем признак Лейбница: если члены знакочередующегося ряда убывают по абсолютной величине и стремятся к нулю при , то ряд сходится (по крайней мере, условно).

В данном случае, если условия признака Лейбница выполнены, то исходный ряд сходится условно (т.к. уже выяснено, что абсолютно он не сходится).

Задача 7. Исследовать на сходимость ряд.

\11.7.1.	11.7.11.
11.7.2.	11.7.12.
11.7.3.	11.7.13.
11.7.4.	11.7.14.
11.7.5.	11.7.15.
11.7.6	11.7.16.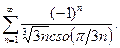
11.7.7. 11.7.8.	11.7.17. 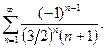11.7.18.
11.7.9.	11.7.19.
11.7.10.	11.7.20.

Постановка задачи 8.

Вычислить сумму знакочередующегося числового ряда , с заданной точностью .

План решения задачи 8.

1. Если и , то для остатка знакочередующегося ряда справедливо неравенство ,т.е. остаток ряда меньше по модулю первого отброшенного члена ряда.

2. Если , то и . Поэтому, решая неравенство , находим количество членов ряда, которое необходимо взять для вычисления суммы ряда с заданной точностью .

3. Непосредственно вычисляем n-ю частичную сумму ряда

Задача 8. Вычислить сумму ряда с точностью .

11.8.1.	11.8.11.
11.8.2.	11.8.12.
11.8.3.	11.8.13.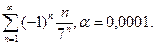
11.8.4.	11.8.14.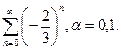
11.8.5.	11.8.15.
11.8.6.	11.8.16.
11.8.7.	11.8.17.
11.8.8.	11.8.18.
11.8.9.	11.8.19.
11.8.10.	11.8.20.

Постановка задач 9-11.

Найти область сходимости функционального ряда

План решения задач 9-11.

При каждом допустимом значении рассматриваем данный ряд как числовой и исследуем его сходимость, применяя теоремы сравнения, признаки Коши, Даламбера и др. Таким образом, находим те значения , при которых данный ряд сходится. Совокупность таких значений образует область сходимости ряда.

При использовании признаков Даламбера или Коши поступаем следующим образом.

1. Находим по одной из формул (если предел существует) или ,где – общий член ряда.

2. Т.к. по признакам Даламбера или Коши ряд сходится при <1 и расходится при >1, находим интервал сходимости, решая неравенство <1.

3. Исследуем поведение ряда в граничных точках интервала сходимости.

Задача 9. Найти область сходимости ряда.

11.9.1.	11.9.11.
11.9.2.	11.9.12.
11.9.3.	11.9.13.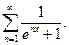
11.9.4.	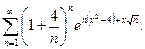11.9.14.
11.9.5.	11.9.15.
11.9.6.	11.9.16.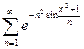
11.9.7.	11.9.17.
11.9.8.	11.9.18.
11.9.9.	11.9.19.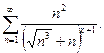
11.9.10.	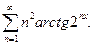11.9.20.

Задача 10. Найти область сходимости ряда.

11.101.	11.10.11.
11.10.2.	11.1012.
11.10.3.	11.1013.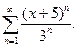
11.10.4.	11.10.14.
11.10.5.	11.10.15.
11.10.6. 11.10.7.	11.10.16. 1.10.17.
11.10.8.	11.10.18.
11.10.9.	11.10.19.
11.10.10.	11.10.20.

Задача 11. Найти область сходимости ряда.

Поиск по сайту: