АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение типового примера. Задача 12.6.Непрерывная случайная величина Х задана функцией распределения

Читайте также:
  1. I. Решение логических задач средствами алгебры логики
  2. II. Решение логических задач табличным способом
  3. III. Разрешение споров в международных организациях.
  4. III. Решение логических задач с помощью рассуждений
  5. MFG/PRO – лучшее решение для крупных и средних промышленных предприятий с дискретным типом производства
  6. V2: ДЕ 55 - Решение линейных неоднородных уравнений со специальной правой частью
  7. Аналитическое решение
  8. Антиполия-противоречие в в законе. Противоречие разрешаясь делает чего то возможным. Отрицание-отрицания ( разрешение противоречия (синтез))
  9. Арбитражное разрешение международных споров в Древней Греции
  10. Арбитражное разрешение международных споров в Древнем Риме
  11. Б) Правовое разрешение конфликтов
  12. В результате получаем общее решение системы

Задача 12.6. Непрерывная случайная величина Х задана функцией распределения

.

Найти для неё 1) функцию плотности распределения вероятностей f(х); 2) коэффициент а; 2) вероятности попадания в интервалы (1,5; 2) и (0,5; 1,3); 3) математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. 1) Для непрерывной случайной величины по определению функции плотности вероятностей F’(х)=f(х). Следовательно,

.

2) Так как , то и 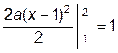, следовательно, а=1.

3) Вероятность попадания случайной величины Х в заданный интервал находится по формуле: Р(α<Х<β)= F(β) – F(α). Так как а=1, то Р(1,5<X<2)= =F(2)-F(1,5)=(2-1)2 – (1,5-1)2 =1 – 0,52=0,75, а Р(0,5<X<1,3)= F(1,3) – F(0,5) = =(1,3 – 1)2 – 0 = 0,09.

4) Математическое ожидание непрерывной случайной величины Х находится по формуле:

.

Так как вне интервала [1, 2] f(x)= 0 и а=1, то М(Х)= = ,

Так как дисперсия непрерывной случайной величины находится по формуле 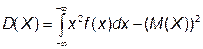, то в нашем случае

.

Среднее квадратическое отклонение случайной величины

= .

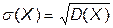Ответ: 1) 1; 2) 0,09; 3) М(Х) = , .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)