 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кореляційна залежність
Кінцевою метою наукового аналізу, зазвичай, є знаходження зв’язків (залежностей) між змінними. Соціального педагога часто цікавить, як пов’язані між собою дві ознаки, які вивчаються, у цій групі осіб. Наприклад:
1. Чи мають учні, які навчилися читати раніше за інших, тенденцію до більш високої успішності в старших класах?
2. Чи є зв’язок між інтелектом батьків та дітей?
3. Чи будуть робітники з більшим стажем роботи мати більшу продуктивність праці? тощо.
Призначення статистики полягає в тому, щоб допомогти досліднику об’єктивно оцінити залежність між змінними.
За характером зв’язку між змінними можна виділити такі види залежностей.
| · функціональні | · причинно-наслідкові | · прямі |
| · кореляційні | · непричинно-наслідкові | · зворотні |
Ознаки (змінні), які вивчаються в ході психолого-педагогічних досліджень, можуть бути пов’язані функціональною або кореляційною залежністю чи можуть бути ніяк не пов’язані між собою.
Досліднику дуже важливо визначити, чи є якийсь зв’язок між змінними, які вивчаються, і, якщо зв’язок є, з’ясувати, яким є характер цього зв’язку (залежності між змінними).
Функціональна залежність має місце, якщо кожному значенню однієї змінної (Х) відповідає цілком певне значення іншої змінної (Y). На рисунку 15 представлено приклади графічного зображення функціональних залежностей.
Приклади функціональних залежностей:
· залежність між швидкістю й пройденою відстанню;
· залежність між вартістю й кількістю купленого на певну суму товару;
· залежність між загальним стажем роботи й стажем роботи на цьому підприємстві тощо.
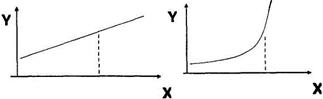
Рис. 15. Приклади графічного зображання
функціональних залежностей
Якщо певному значенню однієї змінної відповідає кілька значень іншої змінної, то має місце кореляційна залежність.
Або, іншими словам, у випадку кореляційної залежності певному значенню однієї величини відповідає комплекс значень іншої, що становить ряд розподілу, при чому, при зміні цієї величини змінюється ряд розподілу та його середнє. Схематичне представлення сили й напрямку кореляції представлено на рисунку 16.
Кореляційний аналіз використовується тоді, коли мета дослідження полягає у знаходженні зв’язку між двома або більш змінними, які спостерігаються у всіх членів вибірки. Завдання кореляційного аналізу – установлення кореляційної залежності між змінними й визначення величини цієї залежності у вигляді коефіцієнтів кореляції.
Коефіцієнти кореляції можуть приймати значення від –1 до +1.
Приклади позитивної кореляції: між IQ та IQ дітей; між ростом батьків та ростом дітей тощо.
Приклади негативної кореляції: між часом, затраченим учнями на перегляд „мильних опер”, та їх оцінками на іспитах.

| Повна позитивна | Повна негативна | Відсутність залежності |
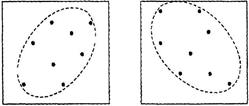
| r = слабка позитивна | r = слабка негативна |

| сильна позитивна | сильна негативна |
Рис. 16. Схематичне представлення сили й напрямку кореляції
Існують два підходи до оцінки сили кореляції. Перший (див. табл. 9) орієнтовано тільки на абсолютну величину коефіцієнта кореляції, а другий – на рівень значущості цього коефіцієнта кореляції при цьому обсязі вибірки (див. табл. 10).
Табл. 9.
Поиск по сайту: