Результати іспиту з історії України

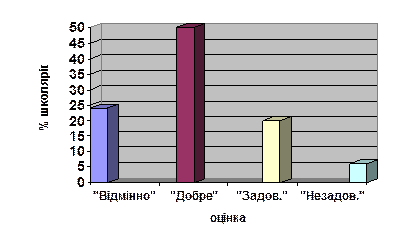Рис. 2. Об’ємний варіант звичайної гістограми

(використано дані таблиці 3)

Результати іспиту з історії України

Рис. 3. Об’ємний варіант кругової діаграми
(використано дані таблиці 3)

Результати іспиту з історії України

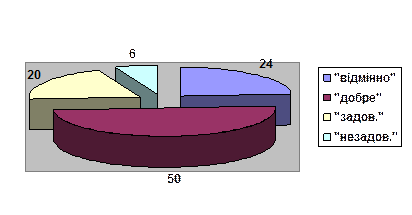
Рис. 4. Об’ємний варіант розрізаної кругової діаграми
(використано дані таблиці 3)

Результати іспиту з історії України (кумулята)

Рис. 5. Крива накопичених частот (кумулята)
(використано дані таблиці 3)

До гістограм, діаграм, графіків, полігонів та інших форм графічного представлення даних висуваються такі загальні вимоги:

· гістограми, діаграми, графіки, полігони тощо повинні обов’язково мати заголовок, з якого повинно бути зрозуміло, які саме дані представлено графічно;

· вісі графіків та частини кругових діаграм повинні бути підписані;

· усі умовні позначки повинні бути зрозумілі або розшифровані в ході опису графіка, гістограми, діаграми тощо.

Міри центральної тенденції

До мір центральної тенденції відносіть моду, медіану й середнє арифметичне значення.

Мода – це те значення, яке у варіаційному ряду результатів вимірів трапляється найбільш часто.

Приклад. У сукупності значень (2, 6, 6, 8, 9, 9, 9, 10) модою є 9. Угода про використання моди:

· у випадку, коли всі значення в групі трапляються однаково часто, прийнято вважати, що група оцінок не має моди, тобто в групі (0,5; 0,5; 1,6; 1,6; 3,9; 3,9) моди немає;

· коли два сусідніх значення мають однакову частоту й вони більше частоти будь-якого іншого значення, мода дорівнює середньому цих двох значень. Отже, мода групи значень (0, 1, 1, 2, 2, 2, 3, 3, 3, 4) дорівнює 2,5;

· якщо 2 несуміжних значення в групі мають рівні частоти й вони більше частот будь-якого значення, то говорять про дві моди. У групі значень (10, 11, 11, 11, 12, 13, 14, 14, 14, 17) модами є 11 та 14; у такому випадку говорять, що група є бімодальною;

Поиск по сайту: